如圖，四邊形ABDC中，∠D=∠ABD=90°，點O為BD的中點，且OA平分∠BAC．
（1）求證：OC平分∠ACD；
（2）求證：OA⊥OC；
（3）求證：AB+CD=AC．
【考點】角平分線的性質．
【答案】見試題解答內容
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/8/6 8:0:9組卷：14706引用：23難度：0.5
相似題
-
1．下面是嘉琪對一個問題的探究過程：
已知：如圖，點D是△ABC內一點，連接BD，CD．
探究：∠BDC與∠A，∠1，∠2之間的數量關系．
解：∵∠BDC+∠DBC+∠BCD=180°（①），
∴∠BDC=180°-∠DBC-∠BCD（等式性質）．
∵∠A+∠1+②+∠DBC+∠BCD=180°，
∴∠A+∠1+∠2=180°-③-∠BCD，
∴∠BDC=∠A+∠1+∠2（④）．
關于嘉琪的答題過程，下列說法不正確的是（ ）發布：2025/5/23 19:30:1組卷：103引用：2難度：0.7 -
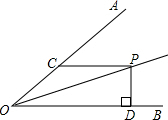2．如圖，∠AOB=30°，OP平分∠AOB，PD⊥OB于D，PC∥OB交OA于C．若PC=10，則OC=，PD=．發布：2025/5/23 10:0:1組卷：410引用：12難度：0.7 -
3．如圖，在Rt△ABC中，∠C=90°，AD平分∠BAC交BC于點D，點E為AB的中點，連接DE，若AB=24，CD=6，則△DBE的面積為 ．發布：2025/5/24 7:0:1組卷：922引用：14難度：0.5