黃金分割比是生活中比較多見的一種長度比值，它能給人許多美感和科學性，我們初中階段學過的許多幾何圖形也有著類似的邊長比例關系．例如我們熟悉的頂角是36°的等腰三角形，其底與腰之比就為黃金分割比5-12，底角平分線與腰的交點為黃金分割點．
（1）如圖1，在△ABC中，∠A=36°，AB=AC，∠ACB的角平分線CD交腰AB于點D，請你證明點D是腰AB的黃金分割點；
（2）如圖2，在△ABC中，AB=AC，若ABBC=5-12，則請你求出∠A的度數；
（3）如圖3，如果在Rt△ABC中，∠ACB=90°，CD為AB上的高，∠A、∠B、∠ACB的對邊分別為a,b,c.若點D是AB的黃金分割點，那么該直角三角形的三邊a,b,c之間是什么數量關系？并證明你的結論．
5
-
1
2
AB
BC
=
5
-
1
2
【答案】見試題解答內容
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：733引用：4難度：0.1
相似題
-
1．如圖，在△ACD中，AD=6，BC=5，AC2=AB（AB+BC），且△DAB∽△DCA，若AD=3AP，點Q是線段AB上的動點，則PQ的最小值是（ ）發布：2025/5/26 1:0:1組卷：4165引用：8難度：0.5 -
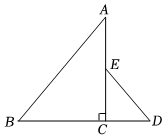2．如圖，在△ABC中∠ACB=90°，AB=2，延長BC到點D，使BC=2CD，若點E是AC的中點，則DE的長為（ ）發布：2025/5/26 0:30:1組卷：233引用：1難度：0.7 -
3．如圖，正方形ABCD中，點F是BC邊上一點，連接AF，以AF為對角線作正方形AEFG，邊FG與正方形ABCD的對角線AC相交于點H，連接DG．以下四個結論：
①∠EAB=∠GAD；
②△AFC∽△AGD；
③2AE2=AH?AC；
④DG⊥AC．
其中正確的個數為（ ）發布：2025/5/26 1:0:1組卷：4461引用：24難度：0.6