【閱讀】
通過構(gòu)造恰當(dāng)?shù)膱D形，可以對線段長度、圖形面積大小等進行比較，直觀地得到一些不等關(guān)系或最值，這是“數(shù)形結(jié)合”思想的典型應(yīng)用．
【理解】
（1）如圖1，AC⊥BC，CD⊥AB，垂足分別為C、D，E是AB的中點，連接CE．已知AD=a,BD=b（0＜a＜b）．
①分別求線段CE、CD的長（用含a、b的代數(shù)式表示）；
②比較大小：CE ＞＞CD（填“＜”、“=”或“＞”），并用含a、b的代數(shù)式表示該大小關(guān)系．
【應(yīng)用】
（2）如圖2，在平面直角坐標(biāo)系xOy中，點M、N在反比例函數(shù)y=1x（x＞0）的圖象上，橫坐標(biāo)分別為m、n.設(shè)p=m+n,q=1m+1n，記l=14pq.
①當(dāng)m=1，n=2時，l=9898；當(dāng)m=3，n=3時，l=11；
②通過歸納猜想，可得l的最小值是 11．請利用圖2構(gòu)造恰當(dāng)?shù)膱D形，并說明你的猜想成立．
1
x
1
m
+
1
n
1
4
9
8
9
8
【考點】反比例函數(shù)綜合題．
【答案】＞；；1；1
9
8
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：3146引用：7難度：0.1
相似題
-
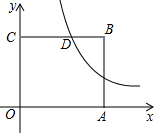1．如圖，在平面直角坐標(biāo)系中，點O為坐標(biāo)原點，正方形OABC的邊OA、OC分別在x軸、y軸上，點B的坐標(biāo)為（2，2），反比例函數(shù)（x＞0，k≠0）的圖象經(jīng)過線段BC的中點D．y=kx
（1）求k的值；
（2）若點P（x,y）在該反比例函數(shù)的圖象上運動（不與點D重合），過點P作PR⊥y軸于點R，作PQ⊥BC所在直線于點Q，記四邊形CQPR的面積為S，求S關(guān)于x的解析式并寫出x的取值范圍．發(fā)布：2025/6/25 6:0:1組卷：1663引用：56難度：0.5 -
2．如圖1，點P為∠MON的平分線上一點，以P為頂點的角的兩邊分別與射線OM，ON交于A，B兩點，如果∠APB繞點P旋轉(zhuǎn)時始終滿足OA?OB=OP2，我們就把∠APB叫做∠MON的智慧角．
（1）如圖2，已知∠MON=90°，點P為∠MON的平分線上一點，以P為頂點的角的兩邊分別與射線OM，ON交于A，B兩點，且∠APB=135°．求證：∠APB是∠MON的智慧角．
（2）如圖1，已知∠MON=α（0°＜α＜90°），OP=2．若∠APB是∠MON的智慧角，連接AB，用含α的式子分別表示∠APB的度數(shù)和△AOB的面積．
（3）如圖3，C是函數(shù)y=（x＞0）圖象上的一個動點，過C的直線CD分別交x軸和y軸于A，B兩點，且滿足BC=2CA，請求出∠AOB的智慧角∠APB的頂點P的坐標(biāo)．3x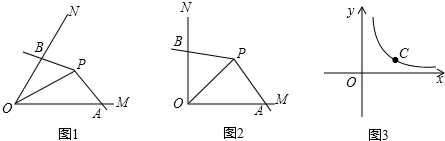
發(fā)布：2025/6/25 6:0:1組卷：3766引用：51難度：0.5 -
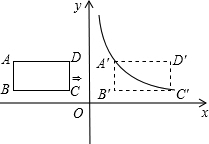3．如圖，在平面直角坐標(biāo)系中，四邊形ABCD是矩形，AD∥x軸，A（-3，），AB=1，AD=2．32
（1）直接寫出B、C、D三點的坐標(biāo)；
（2）將矩形ABCD向右平移m個單位，使點A、C恰好同時落在反比例函數(shù)y=（x＞0）的圖象上，得矩形A′B′C′D′．求矩形ABCD的平移距離m和反比例函數(shù)的解析式．kx發(fā)布：2025/6/25 6:0:1組卷：1947引用：59難度：0.5
相關(guān)試卷