【模型建立】：（1）如圖1，在正方形ABCD中，E，F分別是邊BC，CD上的點，且∠EAF=45°，探究圖中線段EF，BE，DF之間的數量關系．小明的探究思路如下：延長CB到點G，使BG=DF，連接AG，先證明△ADF≌△ABG，再證明△AEF≌△AEG．
①EF，BE，DF之間的數量關系為 BE+DF=EFBE+DF=EF；
②小亮發現這里△ABG可以由△ADF經過一種圖形變換得到，請你寫出這種圖形變換的過程 將△ADF繞A點順時針旋轉90°將△ADF繞A點順時針旋轉90°，像上面這樣有公共頂點，銳角等于較大角的一半，且組成這個較大角的兩邊相等的幾何模型稱為半角模型；
【類比探究】：（2）如圖2，在四邊形ABCD中，AB=AD，∠ABC與∠D互補，E，F分別是邊BC，CD上的點，且∠EAF=12∠BAD，試問線段EF，BE，DF之間具有怎樣的數量關系？判斷并說明理由；
【模型應用】：（3）如圖3，在矩形ABCD中，點E在邊BC上，AD=6，AB=4，∠CAE=45°，求CE的長．
∠
EAF
=
1
2
∠
BAD
【考點】四邊形綜合題．
【答案】BE+DF=EF；將△ADF繞A點順時針旋轉90°
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/5/22 1:30:1組卷：805引用：1難度：0.2
相似題
-
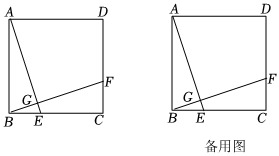1．如圖，正方形ABCD中，點E，F分別在BC，CD上，BE=CF，AE，BF交于點G．
（1）求∠AGF的度數；
（2）在線段AG上截取MG=BG，連接DM，∠AGF的角平分線交DM于點N．
①依題意補全圖形；
②用等式表示線段MN與ND的數量關系，并證明．發布：2025/5/22 14:0:1組卷：1952引用：3難度：0.3 -
2．（1）問題提出
如圖1，在直角△ABC中，∠ACB=90°，AC=6，BC=8，D為邊AB上的一個動點，連接CD，則CD的最小長度為 ．
（2）問題探究
如圖2，在矩形ABCD中，四邊形EFGH為矩形的內接四邊形，點E，F，G，H分別在AD，AB，BC，CD上．FH為對角線，且滿足FH∥AD，若AD=6，AB=4，則四邊形EFGH的面積是否為定值？若是，求出該定值；若不是，請說明理由．
（3）問題解決
如圖3，某果蔬基地規劃修建一片試驗區，并將試驗區劃分為四個區域．按照設計圖的思路，試驗區的平面示意圖為四邊形ABCD，∠ADC=90°，點O在四邊形ABCD的對角線AC上，且滿足OD=50m,CD=110m,OB∥AD，∠OBC=30°，設BO=x m,．S△ABC=ym2
①請寫出y關于x的函數關系式；
②由于果蔬基地占地有限，探究y是否存在最小值．若存在，求出y值；若不存在，請說明理由．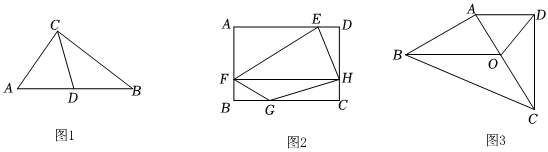
發布：2025/5/22 14:0:1組卷：268引用：2難度：0.1 -
3．問題提出
（1）如圖1，在△ABC中，點D在BC上，連接AD，CD=2BD，則△ABD與△ACD的面積之比為 ；
問題探究
（2）如圖2，在矩形ABCD中，AB=4，BC=8，點P為矩形內一動點，在點P運動的過程中始終有∠APB=45°，求△APB面積的最大值；（結果保留根號）
問題解決
（3）如圖3，某市欲規劃一塊形如平行四邊形ABCD的休閑旅游觀光區，點A為觀光區的入口，并滿足∠BAD=120°，要求在邊BC上確定一點E為觀光區的南門，為了方便市民游覽，修建一條觀光通道AE（觀光通道的寬度不計），且BE=2CE，AE=300米，為了容納盡可能多的游客，要求平行四邊形ABCD的面積最大，請問是否存在滿足上述條件的面積最大的平行四邊形ABCD？若存在，求出平行四邊形ABCD的最大面積；若不存在，請說明理由．（結果保留根號）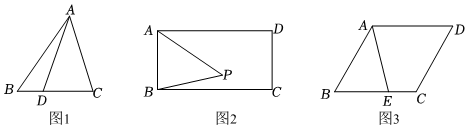
發布：2025/5/22 14:0:1組卷：735引用：4難度：0.1