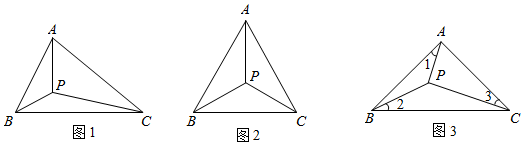
三角形的布洛卡點（ Brocardpoint）是法國數學家和數學教育家克洛爾（A．LCrelle1780-1855）于1816年首次發現，但他的發現并未被當時的人們所注意．1875年布洛卡點被一個數學愛好者法國軍官布洛卡（ Brocard1845-1922）重新發現，并用他的名字命名．如圖1，若△ABC內一點P滿足∠PAB=∠PBC=∠PCA=∠α，則點P是△ABC的布洛卡點，∠α是布洛卡角．
（1）如圖2，點P為等邊三角形ABC的布洛卡點，則布洛卡角的度數是 30°30°；PA、PB、PC的數量關系是 PA=PB=PCPA=PB=PC；
（2）如圖3，點P為等腰直角三角形ABC（其中∠BAC=90°）的布洛卡點，且∠1=∠2=∠3．
①請找出圖中的一對相似三角形，并給出證明；
②若△ABC的面積為52，求△PBC的面積．
5
2
【考點】相似形綜合題．
【答案】30°；PA=PB=PC
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：736引用：5難度：0.2
相似題
-
1．在△ABC中，AB=AC，∠BAC=90°，點D，E分別是AC，BC的中點，點P是射線DE上一點，連接AP，將線段PA繞點P順時針旋轉90°得到線段PM，連接AM，CM．
（1）如圖①，當點P與點D重合時，線段CM與PE的數量關系是 ，∠ACM=°；
（2）如圖②當點P在射線DE上運動時（不與點D，E重合），求的值；PECM
（3）連接PC，當△PCM是等邊三角形時，請直接寫出的值．ACCM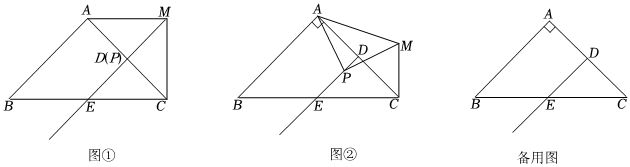
發布：2025/5/23 0:30:1組卷：370引用：2難度：0.1 -
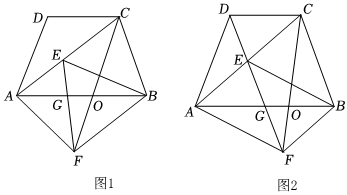2．如圖1，AB=AC=2CD，DC∥AB，將△ACD繞點C逆時針旋轉得到△FCE，使點D落在AC的點E處，AB與CF相交于點O，AB與EF相交于點G，連接BF．
（1）求證：△ABE≌△CAD；
（2）求證：AC∥FB；
（3）若點D，E，F在同一條直線上，如圖2，求的值．（溫馨提示：請用簡潔的方式表示角）ABBC發布：2025/5/23 1:0:1組卷：363引用：2難度：0.4 -
3．已知△ABC是等邊三角形，D是直線AB上的一點．
（1）問題背景：如圖1，點D，E分別在邊AB，AC上，且BD=AE，CD與BE交于點F，求證：∠EFC=60°；
（2）點G，H分別在邊BC，AC上，GH與CD交于點O，且∠HOC=60°．
①嘗試運用：如圖2，點D在邊AB上，且，求OHOG=43的值；ABBD
②類比拓展：如圖3，點D在AB的延長線上，且，直接寫出OHOG=256的值．ABBD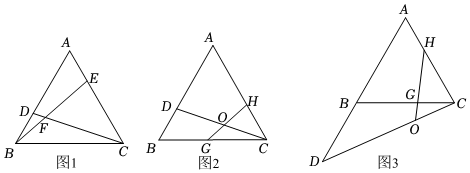
發布：2025/5/23 1:0:1組卷：822引用：3難度：0.2