問題發現:小星發現把幾個圖形拼成一個新的圖形,再通過兩種不同的方法計算同一個圖形的面積,可以得到一個等式,也可以求出一些不規則圖形的面積.
例如,由圖1,可得到等式:(a+2b)(a+b)=a2+3ab+2b2.
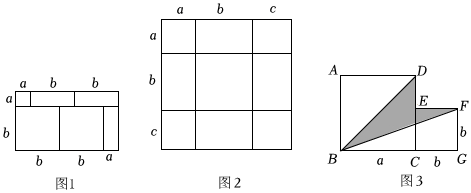
(1)類比探究:如圖2,將幾個面積不等的小正方形與小長方形拼成一個邊長為a+b+c的正方形,通過上面的啟發,你能發現什么結論?請用等式表示出來.
(2)結論應用:已知a+b+c=14,ab+bc+ac=26,求a2+b2+c2的值.
(3)拓展延伸:如圖,將兩個邊長分別為a和b的正方形拼在一起,B,C,G三點在同一直線上,連接BD和BF.若這兩個正方形的邊長滿足a+b=8,ab=14,請求出陰影部分的面積.
【答案】(1)(a+b+c)2=a2+b2+c2+2ab+2bc+2ac;(2)144;(3)11.
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/6/4 8:0:5組卷:103引用:1難度:0.5
相似題
-
1.若x2+3x-5=0,則x3+5x2+x+1=.
發布:2025/6/4 9:30:1組卷:482引用:1難度:0.6 -
2.把代數式通過配湊等手段,得到局部完全平方式再進行有關運算和解題,這種解題方法叫做配方法.如:
①利用配方法分解因式:a2+6a-16.
解:原式=a2+6a+9-9-16=(a+3)2-25=(a+3+5)(a+3-5)=(a+8)(a-2)
②M=2a2+b2-2ab-2a+2,利用配方法求M的最小值.
解:原式=a2-2ab+b2+a2-2a+1+1=(a-b)2+(a-1)2+1
∵(a-b)2≥0,(a-1)2≥0
∴M≥1
∴當a=b=1時,M取得最小值,且最小值為1.
請根據上述材料解決下列問題:
(1)用配方法因式分解:x2-14x+33;
(2)若N=x2+3y2+2xy+2y-1,求N的最值.12發布:2025/6/4 11:0:2組卷:212引用:1難度:0.6 -
3.若x+2y=5,則2x2+8xy+8y2-3=.
發布:2025/6/4 10:30:2組卷:436引用:2難度:0.7


