問題情境
我們知道，“兩條平行線被第三條直線所截，同位角相等，內錯角相等，同旁內角互補”，所以在某些探究性問題中通過“構造平行線”可以起到轉化的作用．
已知三角板ABC中，∠BAC=60°，∠B=30°，∠C=90°，長方形DEFG中，DE∥GF．
問題初探
（1）如圖（1），若將三角板ABC的頂點A放在長方形的邊GF上，BC與DE相交于點M，AB⊥DE于點N，求∠EMC的度數．
分析：過點C作CH∥GF．則有CH∥DE，從而得∠CAF=∠HCA，∠EMC=∠MCH，從而可以求得∠EMC的度數．
由分析得，請你直接寫出：∠CAF的度數為 30°30°，∠EMC的度數為 60°60°．
類比再探
（2）若將三角板ABC按圖（2）所示方式擺放（AB與DE不垂直），請你猜想寫∠CAF與∠EMC的數量關系，并說明理由．
（3）請你總結（1），（2）解決問題的思路，在圖（3）中探究∠BAG與∠BMD的數量關系？并說明理由．
【考點】平行線的判定與性質．
【答案】30°；60°
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/7/4 8:0:9組卷：805引用：5難度：0.6
相似題
-
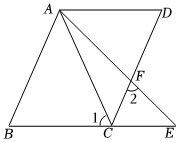1．如圖，已知AB∥CD，∠B=∠D．
（1）求證：AD∥BE；
（2）若∠1=∠2=60°，∠BAC=3∠EAC，求∠DAF的度數．發布：2025/6/7 20:30:1組卷：277引用：6難度：0.7 -
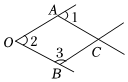2．如圖，一個由4條線段構成的“魚”形圖案，其中∠1=50°，∠2=50°，∠3=130°，找出圖中的平行線，∠ACB的度數，并說明理由．
解：OA∥BC，OB∥AC．
理由：∵∠1=50°，∠2=50°，
∴∠1=∠2（等量代換）
∴OB∥AC． （ ），
∴∠3+∠ACB=180°，（ ），
∴∠ACB=°，
∵∠2=50°，∠3=130°，
∴∠2+∠3=180°，
∴OA∥BC．（ ）．發布：2025/6/7 21:0:1組卷：680引用：6難度：0.9 -
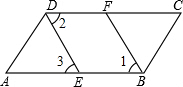3．如圖，∠ABC=∠ADC，BF、DE分別平分∠ABC與∠ADC，DE∥FB．求證：AB∥DC．
請根據條件進行推理，得出結論，并在括號內注明理由．
證明：∵BF、DE分別平分∠ABC與∠ADC，
∴∠1=∠ABC，∠2=12∠ADC．（12）
∵∠ABC=∠ADC，
∴．
∵DE∥FB
∴∠1=∠3，（）
∴∠2=．（等量代換）
∴AB∥CD．（）發布：2025/6/7 21:30:1組卷：637引用：4難度：0.3