完全平方公式：（a+b）2=a2+2ab+b2，（a-b）2=a2-2ab+b2是多項(xiàng)式乘法中的重要公式之一，它經(jīng)過(guò)適當(dāng)變形可以解決很多數(shù)學(xué)問(wèn)題．
例如：若a+b=2，ab=1，求a2+b2的值．
解：a2+b2=（a+b）2-2ab=22-2×1=2．
根據(jù)以上信息回答下列問(wèn)題：
（1）若m+n=3，m2+n2=52，求mn的值；
（2）若a-2b=3，ab=1，求a2+4b2的值；
（3）如圖，點(diǎn)E、F分別是正方形ABCD的邊AD與AB上的點(diǎn)，以AE、AF為邊在正方形內(nèi)部作面積為8的長(zhǎng)方形AFGE，再分別以FG、EG為邊作正方形FGPH和正方形GRQE．若圖中陰影部分的面積為20，求長(zhǎng)方形AFGE的周長(zhǎng)．
【考點(diǎn)】完全平方公式的幾何背景；多項(xiàng)式．
【答案】（1）-8；
（2）13；
（3）12．
（2）13；
（3）12．
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/7/8 8:0:10組卷：654引用：3難度：0.8
相似題
-
1．如圖①，是一個(gè)長(zhǎng)為2m、寬為2n的長(zhǎng)方形，用剪刀沿圖中的虛線（對(duì)稱軸）剪開，把它分成四個(gè)形狀和大小都相同的小長(zhǎng)方形，然后按圖②那樣拼成一個(gè)正方形（中間是空的）．
（1）圖②中畫有陰影的小正方形的邊長(zhǎng)等于多少？
（2）觀察圖②，寫出代數(shù)式（m+n）2，（m-n）2與mn之間的等量關(guān)系；
（3）根據(jù)（2）中的等量關(guān)系解決下面的問(wèn)題：若m+n=7，mn=5，求（m-n）2的值．發(fā)布：2025/6/20 18:0:1組卷：2528引用：11難度：0.7 -
2．有兩個(gè)正方形A，B，現(xiàn)將B放在A的內(nèi)部如圖甲，將A，B并排放置后構(gòu)造新的正方形如圖乙．若圖甲和圖乙中陰影部分的面積分別為和14，則正方形A，B的面積之和為（ ）134發(fā)布：2025/6/20 23:0:1組卷：1909引用：13難度：0.5 -
3．學(xué)習(xí)整式乘法時(shí)，老師拿出三種型號(hào)的卡片，如圖1：A型卡片是邊長(zhǎng)為a的正方形，B型卡片是邊長(zhǎng)為b的正方形，C型卡片是長(zhǎng)和寬分別為a,b的長(zhǎng)方形．
（1）選取1張A型卡片，2張C型卡片，1張B型卡片，在紙上按照?qǐng)D2的方式拼成一個(gè)長(zhǎng)為（a+b）的大正方形，通過(guò)不同方式表示大正方形的面積，可得到乘法公式：．
（2）若用圖1中的8塊C型長(zhǎng)方形卡片可以拼成如圖3所示的長(zhǎng)方形，它的寬為20cm,請(qǐng)你求出每塊長(zhǎng)方形的面積．
（3）選取1張A型卡片，3張C型卡片按圖4的方式不重疊地放在長(zhǎng)方形DEFG框架內(nèi)，已知GF的長(zhǎng)度固定不變，DG的長(zhǎng)度可以變化，圖中兩陰影部分（長(zhǎng)方形）的面積分別表示為S1，S2，若S=S2-S1，則當(dāng)a與b滿足時(shí)，S為定值，且定值為．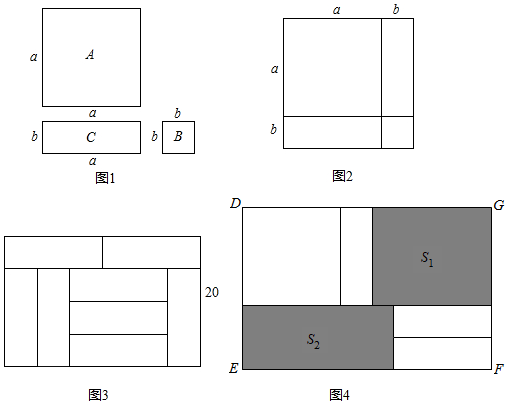
發(fā)布：2025/6/21 0:0:1組卷：531引用：3難度：0.4