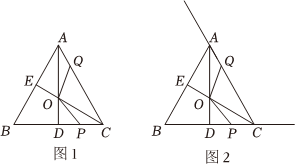
如圖1，△ABC是等邊三角形，AD，CE是△ABC的角平分線，AD與CE相交于點O．點P在線段DC上，點Q在邊AC上，且BP=CQ．連接OP，OQ．
（1）聰聰研究發現OA=OC．
理由如下：因為AD是△ABC的角平分線，且.AB=AC，根據等腰三角形的性質①，可得AD⊥BC，且BD=DC，即AD垂直平分BC，同理，CE垂直平分AB，所以點O是△ABC三邊中垂線的交點，根據線段垂直平分線的性質②，可得OA=OC．
填空：上述證明過程中，①、②兩處的理由分別為 aa和 bb；（填選項前的字母）
a.“三線合一”；b.線段垂直平分線上的點到這條線段兩個端點的距離相等；c.等腰三角形兩個底角相等．
（2）判斷OQ和OP的數量關系，并說明理由；
（3）如圖2，若點P是射線DC上任意一點，點Q在射線CA上，其它條件不變，當△OPC為等腰三角形時，直接寫出∠COQ的度數．
.
A
B
=
AC
【考點】三角形綜合題．
【答案】a；b
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/7/7 8:0:9組卷：254引用：4難度：0.5
相似題
-
1．如圖1和圖2，AD是△ABC中BC邊上的中線，E為AC邊上的一點，過點B作BF∥AC交ED的延長線于點F．
（1）求證：△BDF≌△CDE；
（2）如圖1，若CE=10，AE：BF=2：5，試求AC的長；
（3）如圖2，當E為AC邊的中點時，若△ABC的面積為20，請直接寫出△BDF的面積是多少．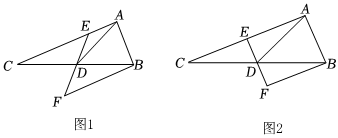
發布：2025/6/8 15:30:1組卷：23引用：1難度：0.4 -
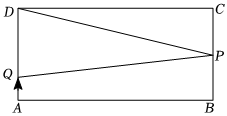2．如圖，在長方形ABCD中，AB=8，AD=4．P是BC的中點，點Q從點A出發，以每秒2個單位長度的速度沿A→D→C→B→A的方向向終點A運動，設點Q運動的時間為x秒．
（1）點Q在運動的路線上和點C之間的距離為4時，x=秒．
（2）若△DPQ的面積為S，用含x的代數式表示S（0≤x＜7）．
（3）若點Q從A出發3秒后，點M以每秒6個單位長度的速度沿A→B→C→D的方向運動，M點運動到達D點后立即沿著原路原速返回到A點，當M與Q在運動的路線上相距不超過4時，請直接寫出相應x的取值范圍．發布：2025/6/8 18:0:1組卷：139引用：1難度：0.2 -
3．如圖1，在平面直角坐標系中，A（a,0），C（b,4），且滿足（a+4）2+
=0，過C作CB⊥x軸于B．b-4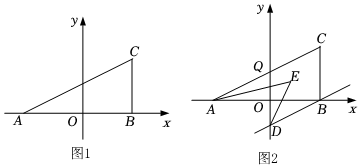
（1）求三角形ABC的面積．
（2）若線段AC交y軸于Q（0，2），在y軸上是否存在點P，使得S△ABC=S△QCP，若存在，求出P的坐標；若不存在，請說明理由．
（3）若過B作BD∥AC交y軸于D，且AE、DE平分∠CAB、∠ODB，如圖2，則∠AED與∠CAB、∠ODB有什么關系，并加以證明．發布：2025/6/8 17:0:2組卷：99引用：3難度：0.3