下面是課河某初中數(shù)學小組探究用不同方法計算三角形面積的片段，請仔細閱讀并完成任務．
試題：在三角形ABC中，BC=4，AC=7.5，AB=8.5，求這個三角形的面積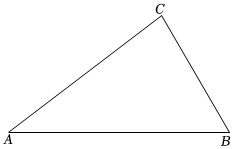． 嘉嘉：過點C作CD⊥AB于D，設CD=x,則分別在Rt△ACD和Rt△BCD中利用勾股定理，最后解關于x的方程，最后再求面積． 琪琪：教材中提到了海倫一秦九韶公式：如果一個三角形的三邊長分別為a,b,c,記 p = a + b + c 2 S = p （ p - a ） （ p - b ） （ p - c ） |
（1）按照嘉嘉的思路，我們還有
2
2
種作輔助線求解的方法；（2）請根據(jù)嘉嘉或者琪琪的思路求出三角形ABC面積；（用一種方法即可）
（3）△ABC的兩條角平分線AD，BE交于點O，求點O到邊AB的距離．
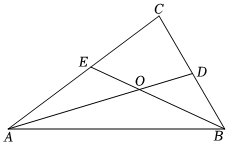
【考點】三角形綜合題．
【答案】2
【解答】
【點評】
聲明：本試題解析著作權屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：61引用：1難度：0.2
相似題
-
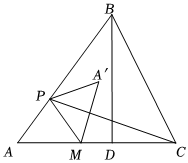1．在△ABC中，BD是AC邊上的高，AD=3，CD=2，BD=4，點M在AD上，且AM=2．動點P從點A出發(fā)，沿折線AB-BD以每秒1個單位長度的速度運動，連結PM，作點A關于直線PM的對稱點A′．設點P的運動時間為t秒（t＞0）．
（1）用含t的代數(shù)式表示線段BP的長；
（2）當點A′在△ABC內(nèi)部時，求t的取值范圍；
（3）連結CP．當CP⊥AB時，求△BCP的面積；
（4）當MA′∥AB時，直接寫出t的值．發(fā)布：2025/6/9 21:30:1組卷：112引用：2難度：0.1 -
2．已知，點P為等邊三角形ABC所在平面內(nèi)一點，且∠BPC=120°．
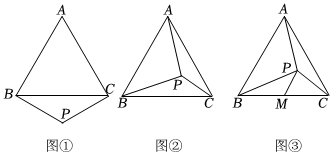
（1）如圖（1），∠ABP=90°，求證：BP=CP；
（2）如圖（2），點P在△ABC內(nèi)部，且∠APB=90°，求證：BP=2CP；
（3）如圖（3），點P在△ABC內(nèi)部，M為BC上一點，連接PM，若∠BPM+∠APC=180°，求證：BM=CM．發(fā)布：2025/6/9 21:30:1組卷：242引用：2難度：0.1 -
3．如圖，點O是等邊△ABC內(nèi)一點，∠AOB=110°，∠BOC=α．△COD為等邊三角形，連接OD、AD．
（1）求證：△BCO≌△ACD；
（2）當α=150°時，試判斷△AOD的形狀，并說明理由；
（3）探究：當α為多少度時，△AOD是等腰三角形？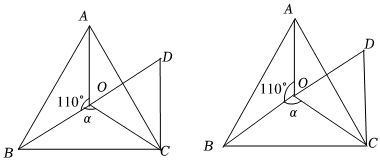
發(fā)布：2025/6/9 23:30:1組卷：57引用：2難度：0.4