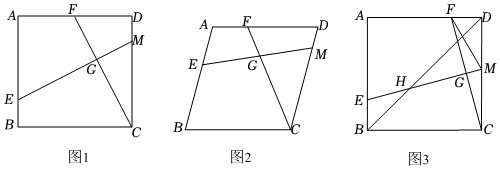
已知，四邊形ABCD為菱形，點(diǎn)E、F、M分別為邊AD、AB、CD上的點(diǎn)，連接CF、ME相交于點(diǎn)G，滿足∠ABC+∠CGE=180°．
（1）如圖1，若∠ABC=90°，求證：EM=CF；
（2）如圖2，若∠ABC≠90°，（1）中結(jié)論是否成立？請(qǐng)說明理由；
（3）如圖3，在（1）的條件下，若∠DCF=15°，點(diǎn)G為CF的中點(diǎn)，BE=2，連接BD交MN于點(diǎn)H，則HG的長(zhǎng)度為 1+31+3．（請(qǐng)直接寫出答案）
2
3
3
【考點(diǎn)】四邊形綜合題．
【答案】1+
3
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2025/6/12 9:30:1組卷：89引用：1難度：0.2
相似題
-
1．如圖，已知矩形ABCD中，AB=4，AD=m,動(dòng)點(diǎn)P從點(diǎn)D出發(fā)，在邊DA上以每秒1個(gè)單位的速度向點(diǎn)A運(yùn)動(dòng)，連接CP，作點(diǎn)D關(guān)于直線PC的對(duì)稱點(diǎn)E，設(shè)點(diǎn)P的運(yùn)動(dòng)時(shí)間為t（s）．
（1）若m=6，求當(dāng)P，E，B三點(diǎn)在同一直線上時(shí)對(duì)應(yīng)的t的值．
（2）已知m滿足：在動(dòng)點(diǎn)P從點(diǎn)D到點(diǎn)A的整個(gè)運(yùn)動(dòng)過程中，有且只有一個(gè)時(shí)刻t,使點(diǎn)E到直線BC的距離等于3，求所有這樣的m的取值范圍．發(fā)布：2025/6/13 13:0:4組卷：3236引用：5難度：0.1 -
2．閱讀材料題：
浙教版九上作業(yè)本①第18頁有這樣一個(gè)題目：已知，如圖一，P是正方形ABDC內(nèi)一點(diǎn)，連接PA、PB、PC，若PC=2，PA=4，∠APC=135°，求PB的長(zhǎng)．
小明看到題目后，思考了許久，仍沒有思路，就去問數(shù)學(xué)老師，老師給出的提示是：將△PAC繞點(diǎn)A順時(shí)針旋轉(zhuǎn)90°得到△P'AB，再利用勾股定理即可求解本題．請(qǐng)根據(jù)數(shù)學(xué)老師的提示幫小明求出圖一中線段PB的長(zhǎng)為．
【方法遷移】：已知：如圖二，△ABC為正三角形，P為△ABC內(nèi)部一點(diǎn)，若PC=1，PA=2，PB=，求∠APB的大小．3
【能力拓展】：已知：如圖三，等腰三角形ABC中∠ACB=120°，D、E是底邊AB上兩點(diǎn)且∠DCE=60°，若AD=2，BE=3，求DE的長(zhǎng)．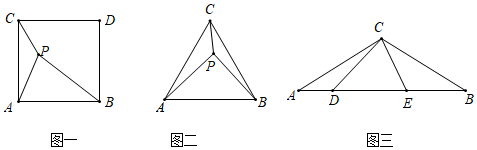
發(fā)布：2025/6/13 9:0:1組卷：508引用：3難度：0.1 -
3．已知四邊形ABCD是正方形，點(diǎn)F為射線AD上一點(diǎn)，連接CF并以CF為對(duì)角線作正方形CEFG，連接BE，DG．
（1）如圖1，當(dāng)點(diǎn)F在線段AD上時(shí)，求證：BE=DG；
（2）如圖1，當(dāng)點(diǎn)F在線段AD上時(shí)，求證：CD-DF=BE；2
（3）如圖2，當(dāng)點(diǎn)F在線段AD的延長(zhǎng)線上時(shí)，請(qǐng)直接寫出線段CD，DF與BE間滿足的關(guān)系式．發(fā)布：2025/6/13 7:0:2組卷：429引用：3難度：0.2