“楊輝三角”揭示了(a+b)n(n為非負整數)展開式的各項系數的規律.在歐洲,這個表叫做帕斯卡三角形.帕斯卡是在1654年發現這一規律的,比楊輝要遲393年,比賈憲遲600年.請仔細觀察“楊輝三角”中每個數字與上一行的左右兩個數字之和的關系:
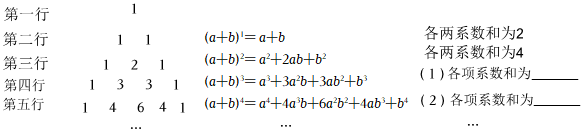
根據上述規律,完成下列各題:
(3)將(a+b)5展開后,各項的系數和為 3232.
(4)(a+b)6=a6+6a5b+15a4b2+20a3b3+15a2b4+6ab5+b6a6+6a5b+15a4b2+20a3b3+15a2b4+6ab5+b6.
(5)將(a+b)n展開后,各項的系數和為 2n2n.
如圖是世界上著名的“萊布尼茨三角形”,類比“楊輝三角”,根據你發現的規律,回答下列問題:

(6)若(m,n)表示第m行,從左到右數第n個數,如(4,2)表示第四行第二個數是112,則(6,2)表示的數是 130130,(8,3)表示的數是 11681168.
1
12
1
30
1
30
1
168
1
168
【答案】32;a6+6a5b+15a4b2+20a3b3+15a2b4+6ab5+b6;2n;;
1
30
1
168
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/6/27 10:35:59組卷:246引用:1難度:0.6
相似題
-
1.a-b=3,ab=10,則a2+b2的值是 .
發布:2025/6/7 19:30:2組卷:39引用:2難度:0.7 -
2.已知x+y=5,xy=-14,求x-y=.
發布:2025/6/7 17:0:1組卷:127引用:1難度:0.8 -
3.我國古代數學的許多發現都曾位居世界前列,如圖1的“楊輝三角”就是其中的一例.如圖2,某同學發現楊輝三角給出了(a+b)n(n為正整數)的展開式(按a的次數由大到小的順序排列)的系數規律,例如,在三角形中第三行的三個數1,2,1,恰好對應(a+b)2=a2+2ab+b2展開式中各項的系數;第四行的四個數1,3,3,1,恰好對應著(a+b)3=a3+3a2b+3ab2+b3展開式中各項的系數等等.

(1)填出(a+b)4展開式中共有 項,第三項是 .
(2)直接寫出(a+b)5的展開式.
(3)利用上面的規律計算(不用材料中的規律計算不給分):25-5×24+10×23-10×22+5×2-1.發布:2025/6/7 19:30:2組卷:245引用:3難度:0.5


