我國魏晉時期的數學家劉徽首創“割圓術”：“割之彌細，所失彌少，割之又割，以至于不可割，則與圓合體，而無所失矣”．即通過圓內接正多邊形割圓，從正六邊形開始，每次邊數成倍增加，依次可得圓內接正十二邊形，內接正二十四邊形，…，邊數越多割得越細，正多邊形的周長就越接近圓的周長．再根據“圓周率等于圓周長與該圓直徑的比”來計算圓周率．設圓的半徑為R，圖1中圓內接正六邊形的周長l6=6R，則π≈l62R=3．再利用圖2圓的內接正十二邊形計算圓周率，首先要計算它的周長，下列結果正確的是（ ）
l
6
2
R
【答案】A
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/12/7 3:0:2組卷：379引用：5難度：0.5
相似題
-
1．如圖1是自動卸貨汽車卸貨時的狀態圖，圖2是其示意圖．汽車的車廂采用液壓機構、車廂的支撐頂桿BC的底部支撐點B在水平線AD的下方，AB與水平線AD之間的夾角是5°，卸貨時，車廂與水平線AD成60°，此時AB與支撐頂桿BC的夾角為45°，若AC=2米，求BC的長度．（結果保留一位小數）
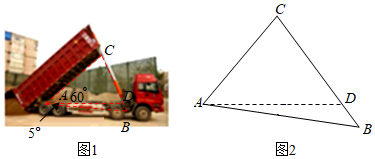
（參考數據：sin65°≈0.91，cos65°≈0.42，tan65°≈2.14，sin70°≈0.94，cos70°≈0.34，tan70°≈2.75，≈1.41）2發布：2025/5/25 6:0:1組卷：1993引用：17難度：0.6 -
2．釣魚是修身養性的戶外休閑運動，閑暇之余，流連于江河湖泊之間，鳥語花香，玉樹蔥蔥，享受大自然，怡然自樂…，“勸君莫食三月鯽，萬千魚仔魚腹中”，釣魚是一種心情，釣獲放流是一種境界！
如圖一靜待鯉魚上鉤：AB是魚竿，BC、CD是魚線，EH是水面，點B、點C分別在矩形EFDH的一組鄰邊上，AF⊥EH，AB=8米，AF=7米，CH=0.5米，∠ABE=30°，∠HBC=4.4°．
如圖二揚竿中魚：魚竿AB彎成圓弧，其圓心恰好是點O，魚線OB由于受到拉力作用，長度變為原來的1.2倍，即：OB=1.2（BC+CD）．
若∠AOB的度數超過45°，魚竿將有折斷的危險，請你通過計算說明：是否有斷竿跑魚的危險？
（參考數據：π取3，sin4.4°≈，cos4.4°≈0.997，tan4.4°≈3.096）113發布：2025/5/25 5:0:4組卷：114引用：1難度：0.4 -
3．如圖①，將“歡迎光臨”門掛傾斜放置時，測得掛繩的一段AC=30cm.另一段BC=20cm.已知兩個固定扣之間的距離AB=30cm.
（1）求點C到AB的距離；
（2）如圖②，將該門掛扶“正”（即AC=BC），求∠CAB的度數．
（參考數據：sin49°≈0.75，cos41°≈0.75，tan37°≈0.75，cos53°≈0.6，tan53°≈）43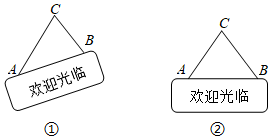
發布：2025/5/25 4:30:1組卷：442引用：8難度：0.5
相關試卷