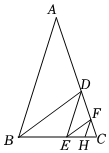
我們將頂角為36°的等腰三角形稱為黃金三角形（底邊和腰的比值為黃金分割比）．如圖，已知AB=1，△ABC為第一個黃金三角形，△BDC為第二個黃金三角形，…，依次類推則第2021個黃金三角形的底邊長為（ ）
【考點】黃金分割；規(guī)律型：圖形的變化類．
【答案】B
【解答】
【點評】
聲明：本試題解析著作權屬菁優(yōu)網所有，未經書面同意，不得復制發(fā)布。
發(fā)布：2024/9/26 20:0:1組卷：164引用：2難度：0.5
相似題
-
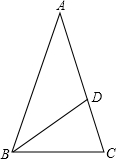1．如圖，△ABC中，AB=AC，∠A=36°，BD平分∠ABC交AC于點D，點D為AC的黃金分割點（AD＞CD），AC=6，則CD=．發(fā)布：2025/1/20 8:0:1組卷：122引用：2難度：0.7 -
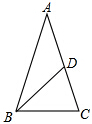2．頂角是36°的等腰三角形稱為黃金三角形，如圖，在△ABC中，AB=AC=1，∠A=36°，BD是△ABC的角平分線，那么AD=．發(fā)布：2025/1/20 8:0:1組卷：104引用：0難度：0.9 -
3．已知點C是線段AB的黃金分割點，且BC＞AC，若AB=2，則BC的值為（ ）
發(fā)布：2024/12/21 23:30:7組卷：193引用：3難度：0.6