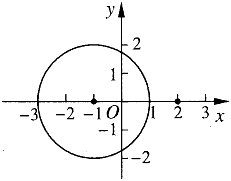
如圖所示，某電子監控安裝在點（-1，0），監控范圍為半徑r=2的一個圓．
（1）試寫出這個圓的一般式方程；
（2）有人經過點（2，0），斜率為-1的直線l上活動，試問監控能否發現？為什么？

【答案】（1）x²+y²+2x-3=0；（2）監控不能發現，理由見解答.

【解答】

【點評】

聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。

發布：2024/6/27 10:35:59組卷：31引用：1難度：0.7

相似題

1．已知圓C過點P（-1，-1），且與圓M：（x-2）²+（y+2）²=r²（r＞0）關于直線x-y-2=0對稱。
（1）求圓C、圓M的方程；
（2）過點P作圓C的兩條相交直線PA、PB，且PA、PB的斜率互為相反數，試判斷直線OP與AB的斜率是否相等，說明理由。
發布：2025/1/2 22:0:1組卷：25引用：2難度：0.5
解析
2．若直線y=x+b與曲線
y
=
4
-
x
2
有一個交點，則實數b的取值范圍是

．
發布：2024/7/26 8:0:9組卷：25引用：1難度：0.5
解析
3．已知圓C的圓心為直角坐標系原點，且與直線
l
1
：
x
+
y
+
4
2
=
0
相切．
（1）求圓C的方程；
（2）P是直線l₂：x=8上任意點，過點P引圓C的兩條切線PA，PB，切點分別為A和B，求證：過A、B兩點的直線恒過定點．
發布：2024/6/27 10:35:59組卷：11引用：1難度：0.7
解析

相關試卷

如圖所示，某電子監控安裝在點（-1，0），監控范圍為半徑r=2的一個圓．（1）試寫出這個圓的一般式方程；（2）有人經過點（2，0），斜率為-1的直線l上活動，試問監控能否發現？為什么？