閱讀理解：
我們知道在直角三角形中，有無數(shù)組勾股數(shù)，例如5，12，13；9，40，41；…但其中也有一些特殊的勾股數(shù)，例如：3，4，5是三個連續(xù)正整數(shù)組成的勾股數(shù)．
解決問題：
（1）在無數(shù)組勾股數(shù)中，是否存在三個連續(xù)偶數(shù)能組成勾股數(shù)？若存在，試寫出一組勾股數(shù)；
（2）在無數(shù)組勾股數(shù)中，是否還存在其他的三個連續(xù)正整數(shù)能組成勾股數(shù)？若存在，求出勾股數(shù)；若不存在，說明理由．
【考點】勾股定理的證明．
【答案】（1）存在，6、8、10；
（2）不存在，理由詳見解答．
（2）不存在，理由詳見解答．
【解答】
【點評】
聲明：本試題解析著作權屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復制發(fā)布。
發(fā)布：2025/6/17 4:30:1組卷：109引用：1難度：0.6
相似題
-
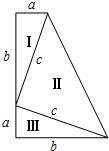1．如圖，三個直角三角形（Ⅰ，Ⅱ，Ⅲ）拼成一個直角梯形（兩底分別為a、b,高為a+b），利用這個圖形，小明驗證了勾股定理．請你填寫計算過程中留下的空格：
S梯形=（上底+下底）?高=12（a+b）?（a+b），即S梯形=12（）①12
S梯形=Ⅰ+Ⅱ+Ⅲ（羅馬數(shù)字表示相應圖形的面積）
=++，即S梯形=（）②12
由①、②，得a2+b2=c2．發(fā)布：2025/6/17 20:30:2組卷：305引用：2難度：0.7 -
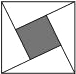2．“趙爽弦圖”是四個全等的直角三角形與中間一個正方形拼成的大正方形．如圖，每一個直角三角形的兩條直角邊的長分別是3和6，則中間小正方形與大正方形的面積差是（ ）發(fā)布：2025/6/17 19:30:1組卷：3427引用：3難度：0.5 -
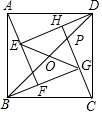3．如圖，四個全等的直角三角形拼成“趙爽弦圖”，得到正方形ABCD與正方形EFGH．連接EG，BD相交于點O，BD與HC相交于點P．若GO=GP，則的值是（ ）S正方形ABCDS正方形EFGH發(fā)布：2025/6/17 22:0:1組卷：5295引用：33難度：0.6