在平面直角坐標系xOy中，⊙O的半徑為1，對于⊙O和⊙O外的點P，給出如下的定義：若在⊙O上存在一點Q，使得P、Q兩點間的距離小于或等于1，則稱P為⊙O的近距點．
（1）在點P1（1，1），P2（-12，32），P3（0，-12），P4（2，1）中，⊙O的近距點是 P1P1；
（2）若直線l：y=x+b上存在⊙O的近距點，直接寫出字母b的取值范圍；
（3）若點P在直線y=x+1上，且點P是⊙O的近距點，求點P橫坐標xP的取值范圍．
（
-
1
2
，
3
2
）
-
1
2
【考點】圓的綜合題．
【答案】P1
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/4/20 14:35:0組卷：28引用：1難度：0.3
相似題
-
1．小亮學習了圓周角定理的推論“圓內接四邊形對角互補”后，勇于思考大膽創新，并結合三角形的角平分線的性質進行了以下思考和發現：
（1）①如圖1，四邊形ABCD是⊙O的內接四邊形，若∠B=85°，則∠ADE=；
②如圖2，在△ABC中，BE，CE分別平分∠ABC和∠ACD，BE，CE相交于點E，∠A=42°，則∠E=°；
（2）小亮根據這個發現，又進行了以下深入研究：
如圖3，四邊形ABCD內接于⊙O，對角線BD是⊙O的直徑，AC=BC，點F是弧AD的中點，求∠E的度數[（1）中的結論可直接用]．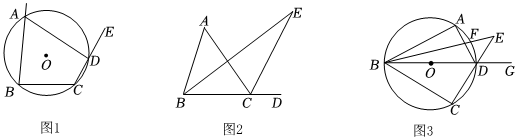
發布：2025/5/24 19:30:1組卷：127引用：1難度：0.4 -
2．如圖1，在等腰△ABC中，AB=AC，AO平分∠BAC且交BC于點O，AB與⊙O相切于點D，OC交⊙O于點H，連接OD．
（1）求證：AC是⊙O的切線；
（2）延長DO、AC交于點E，若CE=OC，求證：OA=OE；
（3）在（2）的條件下，連接DH交AO于點K，若OK?AK=8-12，求⊙O的半徑并直接寫出DK?HK的值．3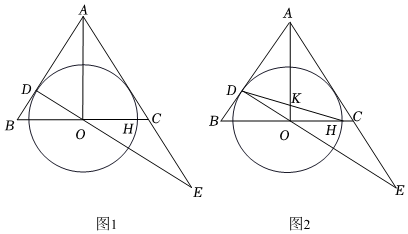
發布：2025/5/24 19:30:1組卷：184引用：1難度：0.1 -
3．點E為正方形ABCD的邊CD上一動點，直線AE與BD相交于點F，與BC的延長線相交于點G．
（1）如圖①，若正方形的邊長為2，設DE=x,△DEG的面積為y,求y與x的函數關系；
（2）如圖②，求證：CF是△ECG的外接圓的切線；
（3）如果把正方形ABCD換成是矩形或菱形，（2）的結論是否仍然成立？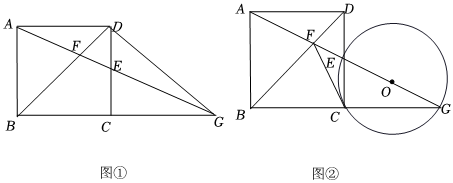
發布：2025/5/24 18:30:1組卷：91引用：1難度：0.1