如圖，已知B（-1，0），C（1，0），A為y軸正半軸上一點(diǎn)，點(diǎn)D為第二象限一動(dòng)點(diǎn)，E在BD的延長(zhǎng)線上，CD交AB于F，且∠BDC=2∠BAO．
（1）求證：∠ABD=∠ACD；
（2）求證：AD平分∠CDE；
（3）若在D點(diǎn)運(yùn)動(dòng)的過(guò)程中，始終有DC=DA+DB，在此過(guò)程中，∠BAC的度數(shù)是否變化？如果變化，請(qǐng)說(shuō)明理由；如果不變，請(qǐng)求出∠BAC的度數(shù)．
【考點(diǎn)】三角形綜合題．
【答案】（1）證明見(jiàn)解答；
（2）證明見(jiàn)解答；
（3）∠BAC的度數(shù)不變，為60°．
（2）證明見(jiàn)解答；
（3）∠BAC的度數(shù)不變，為60°．
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書(shū)面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/4/20 14:35:0組卷：967引用：9難度：0.4
相似題
-
1．如圖1，△ABC和△CDE都是等邊三角形，且A，C，E在同一條直線上，分別連接AD，BE．
（1）求證：AD=BE；
（2）如圖2，連接BD，若M，N，Q分別為AB，DE，BD的中點(diǎn)，過(guò)N作NP⊥MN與MQ的延長(zhǎng)線交于P，求證：MP=AD；
（3）如圖3，設(shè)AD與BE交于F點(diǎn)，點(diǎn)M在AB上，MG∥AD，交BE于H，交CF的延長(zhǎng)線于G，試判斷△FGH的形狀．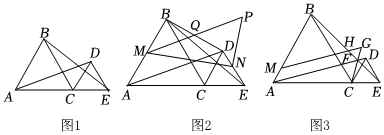
發(fā)布：2025/5/24 17:0:2組卷：45引用：1難度：0.1 -
2．仔細(xì)閱讀以下內(nèi)容解決問(wèn)題：第24屆國(guó)際數(shù)學(xué)家大會(huì)會(huì)標(biāo)，設(shè)兩條直角邊的邊長(zhǎng)為a,b,則面積為ab,四個(gè)直角三角形面積和小于正方形的面積得：a2+b2≥2ab,當(dāng)且僅當(dāng)a=b時(shí)取等號(hào)．在a2+b2≥2ab中，若a＞0，b＞0，用12、a代替a,b得，a+b≥2b，即ab（*），我們把（*）式稱為基本不等式．利用基本不等式我們可以求這個(gè)式子的最大最小值．我們以“已知x為實(shí)數(shù)，求y=a+b2≥ab的最小值”為例給同學(xué)們介紹．x2+4x2+1
解：由題知y=，x2+1+3x2+1=x2+1+3x2+1
∴＞0，x2+1＞0，3x2+1
∴y=，當(dāng)且僅當(dāng)x2+1+3x2+1≥2x2+1?3x2+1=23時(shí)取等號(hào)，即當(dāng)x=x2+1=3x2+1時(shí)，函數(shù)的最小值為22．3
總結(jié)：利用基本不等式（a＞0，b＞0）求最值，若ab為定值．則a+b有最小值．a+b2≥ab
請(qǐng)同學(xué)們根據(jù)以上所學(xué)的知識(shí)求下列函數(shù)的最值，并求出取得最值時(shí)相應(yīng)x的取值．
（1）若x＞0，求y=2x+的最小值；2x
（2）若x＞2，求y=x+的最小值；1x-2
（3）若x≥0，求y=的最小值．x+4x+13x+2發(fā)布：2025/5/24 19:30:1組卷：236引用：3難度：0.5 -
3．問(wèn)題情景：已知在△ABC中，AB=AC，∠BAC=α，過(guò)點(diǎn)A作AD⊥BC于點(diǎn)D，點(diǎn)P為直線BC上一點(diǎn)（不與點(diǎn)B、C重合），過(guò)點(diǎn)P作PM⊥AB于點(diǎn)M，PN⊥AC于點(diǎn)N．
（1）觀察猜想
如圖1，若α=60°，P在線段BC上時(shí)，線段PM、PN、AD的數(shù)量關(guān)系是 ．
（2）類比探究
如圖2，若α=90°，P在線段BC上時(shí)，判斷線段PM、PN、AD的數(shù)量關(guān)系，并說(shuō)明理由．
（3）問(wèn)題解決
若α=120°，點(diǎn)P在線段BC兩端點(diǎn)的外端，且AD=2，請(qǐng)直接寫(xiě)出PM-PN的值．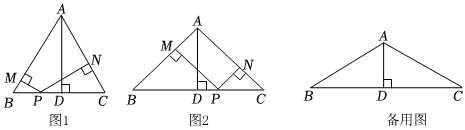
發(fā)布：2025/5/24 20:0:2組卷：74引用：1難度：0.3