在平面直角坐標系xOy中，對于點P和直線y=1，給出如下定義：若點P在直線y=1上，且以點P為頂點的角是45°，則稱點P為直線y=1的“關聯(lián)點”．
（1）若在直線x=1上存在直線y=1的“關聯(lián)點”P，則點P的坐標為 （1，1）（1，1）；
（2）過點P（2，1）作兩條射線，一條射線垂直于x軸，垂足為A；另一條射線交x軸于點B，若點P為直線y=1的“關聯(lián)點”．求點B的坐標；
（3）以點O為圓心，1為半徑作圓，若在⊙O上存在點N，使得∠OPN的頂點P為直線y=1的“關聯(lián)點”．則點P的橫坐標a的取值范圍是 -1≤a≤1-1≤a≤1．
【考點】圓的綜合題．
【答案】（1，1）；-1≤a≤1
【解答】
【點評】
聲明：本試題解析著作權屬菁優(yōu)網所有，未經書面同意，不得復制發(fā)布。
發(fā)布：2024/4/20 14:35:0組卷：437引用：2難度：0.1
相似題
-
1．如圖，AB為⊙O的直徑，弦CD⊥AB于點E，G為劣弧AD上一動點，AG與CD的延長線交于點F，連接AC、AD、CG、DG．tan∠DGF=m（m為常數(shù)，且m＞1）．
（1）求證：∠AGC=∠DGF；
（2）求的值（用含m的式子表示）；AG?AFCE2
（3）設∠GDC-∠GCD=α，∠F=β．
①求α與β的數(shù)量關系；
②當α=90°，且S△CAG=S△CAD時，求m的值．發(fā)布：2025/5/21 21:0:1組卷：1387引用：3難度：0.3 -
2．問題背景
（1）如圖（1）△ABC內接于⊙O，過A作⊙O的切線l,在l上任取一個不同于點A的點P，連接PB、PC，比較∠BPC與∠BAC的大小，并說明理由．
問題解決
（2）如圖（2），A（0，2），B（0，4），在x軸正半軸上是否存在一點P，使得cos∠APB最小？若存在，求出P點坐標，若不存在，請說明理由．
拓展應用
（3）如圖（3），在四邊形ABCD中，AB∥CD，AD⊥CD于D，E是AB上一點，AE=AD，P是DE右側四邊形ABCD內一點，若AB=8，CD=11，tan∠C=2，S△DEP=9，求sin∠APB的最大值．
發(fā)布：2025/5/21 21:0:1組卷：915引用：2難度：0.2 -
3．問題提出：
（1）如圖1，⊙O是△ABC的外接圓，∠A=60°，BC=4，則⊙O半徑長等于 ；
問題探究：
（2）如圖2，在矩形ABCD中，AB=4，若在邊CD上存在一點P，使得∠APB=90°，求矩形ABCD面積的最大值；
問題解決：
（3）如圖3，是一個矩形廣場，其中AB=60m,BE足夠長．為了方便居民生活，促進經濟發(fā)展，街道計劃在矩形內部修建一個面積盡量大的交易市場ABCD，其中C，D分別在邊BE，AF上，且∠BCD=45°．在具體施工中安全聯(lián)防小組要求在CD上找到一點Q，使得∠AQB=45°，以便安裝攝像頭對市場進行安全監(jiān)管．請問滿足上面要求的市場ABCD是否存在，若存在，請求出市場ABCD面積的最大值；若不存在，請說明理由．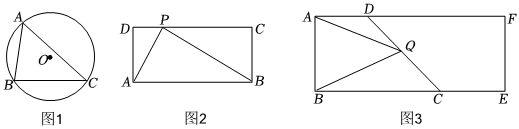
發(fā)布：2025/5/21 21:0:1組卷：357引用：1難度：0.4