問題提出：
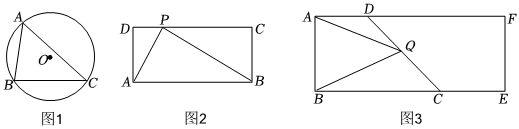
（1）如圖1，⊙O是△ABC的外接圓，∠A=60°，BC=4，則⊙O半徑長等于 433433；
問題探究：
（2）如圖2，在矩形ABCD中，AB=4，若在邊CD上存在一點P，使得∠APB=90°，求矩形ABCD面積的最大值；
問題解決：
（3）如圖3，是一個矩形廣場，其中AB=60m,BE足夠長．為了方便居民生活，促進(jìn)經(jīng)濟(jì)發(fā)展，街道計劃在矩形內(nèi)部修建一個面積盡量大的交易市場ABCD，其中C，D分別在邊BE，AF上，且∠BCD=45°．在具體施工中安全聯(lián)防小組要求在CD上找到一點Q，使得∠AQB=45°，以便安裝攝像頭對市場進(jìn)行安全監(jiān)管．請問滿足上面要求的市場ABCD是否存在，若存在，請求出市場ABCD面積的最大值；若不存在，請說明理由．
4
3
3
4
3
3
【考點】圓的綜合題．
【答案】
4
3
3
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2025/5/21 21:0:1組卷：357引用：1難度：0.4
相似題
-
1．如圖1，在矩形ABCD中，AB=4，BC=6，點E，F(xiàn)分別在邊AD，CD上，且∠ABE=∠CBF，延長BE交CD的延長線于點G，H為BG中點，連結(jié)CH分別交BF，AD于點M，N．
（1）求證：BF⊥CH．
（2）當(dāng)FG=9時．
①求tan∠FBG的值．
②在線段CH上取點P，以E為圓心，EP為半徑作⊙E（如圖2），當(dāng)⊙E與四邊形ABMN某一邊所在直線相切時，求所有滿足條件的HP的長．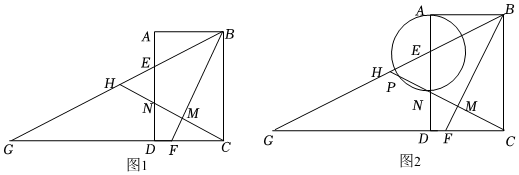
發(fā)布：2025/5/22 3:0:1組卷：687引用：2難度：0.4 -
2．（1）如圖1，⊙A的半徑為1，AB=2.5，點P為⊙A上任意一點，則BP的最小值為 ；
（2）如圖2，已知矩形ABCD，點E為AB上方一點，連接AE，BE，作EF⊥AB于點F，點P是△BEF的內(nèi)心，求∠BPE的度數(shù)；
（3）如圖3，在（2）的條件下，連接AP，CP，若矩形的邊長AB=6，BC=4，BE=BA，求此時CP的最小值．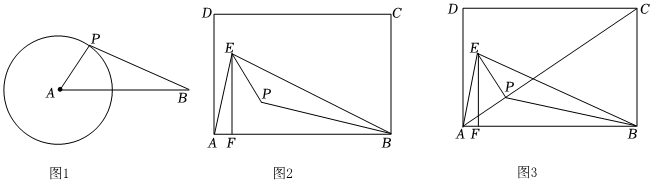
發(fā)布：2025/5/22 4:30:1組卷：311引用：2難度：0.3 -
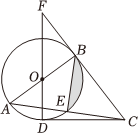3．如圖，Rt△ABC中，∠ABC=90°，以AB為直徑作⊙O，交AC于點E，點D為⊙O上一點，且CD=CB．連接DO并延長交CB的延長線于點F．
（1）求證：CD是⊙O的切線．
（2）若AB=BC=4，連接BE．
①求圖中陰影部分的面積；
②求BF的長．發(fā)布：2025/5/22 4:0:7組卷：139引用：2難度：0.1
相關(guān)試卷