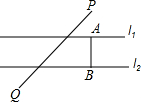
如圖，已知直線l₁∥l₂，l₁、l₂之間的距離為8，點P到直線l₁的距離為6，點Q到直線l₂的距離為4，PQ=4
30
，在直線l₁上有一動點A，直線l₂上有一動點B，滿足AB⊥l₂，且PA+AB+BQ最小，此時PA+BQ=
16
16
．

【答案】16

【解答】

【點評】

聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。

發布：2025/5/25 8:0:2組卷：3006引用：5難度：0.3

相似題

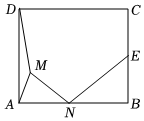1．如圖，在矩形ABCD中，AB=4，AD=2
3
，點E為BC的中點，動點M在矩形內部，連接AM，DM，且∠ADM+∠DAM=30°，點N為AB上一個動點，連接MN，EN，則MN+EN的最小值為
．
發布：2025/5/25 15:0:2組卷：143引用：4難度：0.4
解析
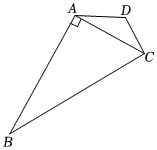2．如圖，四邊形ABCD中，∠D=120°，∠B=30°，且AB⊥AC，AD+DC=6，則四邊形ABCD周長的最小值是
．
發布：2025/5/25 13:30:1組卷：65引用：2難度：0.6
解析
3．如圖，在直角坐標系中，點A（1，1），B（3，3）是第一象限角平分線上的兩點，點C的縱坐標為1，且CA=CB，在y軸上取一點D，連接AC，BC，AD，BD，使得四邊形ACBD的周長最小，這個最小周長的值為
．
發布：2025/5/25 16:0:2組卷：3460引用：10難度：0.4
解析

相關試卷

如圖，已知直線l1∥l2，l1、l2之間的距離為8，點P到直線l1的距離為6，點Q到直線l2的距離為4，PQ=430，在直線l1上有一動點A，直線l2上有一動點B，滿足AB⊥l2，且PA+AB+BQ最小，此時PA+BQ=1616．