問題探究
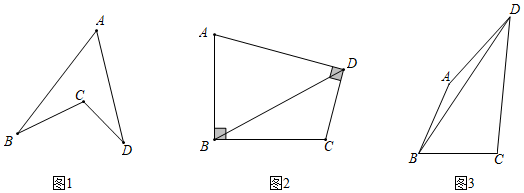
（1）如圖①，已知∠A=45°，∠ABC=30°，∠ADC=40°，則∠BCD的大小為 115°115°；
（2）如圖②，在四邊形ABCD中，AB=BC，∠ABC=∠ADC=90°，對角線BD=6，求四邊形ABCD的面積；小明這樣來計算，延長DC，使得CE=AD，連接BE，通過證明△ABD≌△CBE，從而可以計算四邊形ABCD的面積，請你將小明的方法完善，并計算四邊形ABCD的面積；
問題解決
（3）如圖③，四邊形ABCD是正在建設(shè)的城市花園，其中AB=BC，∠ABC=60°，∠ADC=30°，DC=40米，AD=30米，請計算出對角線BD的長度．
【考點】四邊形綜合題．
【答案】115°
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：207引用：1難度：0.1
相似題
-
1．如圖，點E，F(xiàn)分別在正方形ABCD的邊CD，BC上，且DE=CF，點P在射線BC上（點P不與點F重合）．將線段EP繞點E順時針旋轉(zhuǎn)90°得到線段EG，過點E作GD的垂線QH，垂足為點H，交射線BC于點Q．
（1）如圖1，若點E是CD的中點，點P在線段BF上，
①PQ=；
②線段BP，QC，EC的數(shù)量關(guān)系為 ．
（2）如圖2，若點E不是CD的中點，點P在線段BF上，判斷（1）中的結(jié)論是否仍然成立，若成立，請寫出證明過程；若不成立，請說明理由．
（3）正方形ABCD的邊長為9，DE=DC，QC=2，請直接寫出線段BP的長．13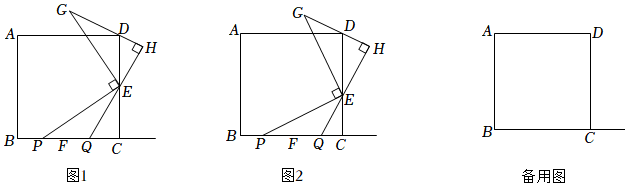
發(fā)布：2025/5/25 3:30:2組卷：544引用：4難度：0.4 -
2．背景閱讀：
早在三千多年前，我國周朝數(shù)學(xué)家商高就提出：將一根直尺折成一個直角，如果勾等于三，股等于四，那么弦就等于五，即“勾三、股四、弦五”．它被記載與我國古代著名數(shù)學(xué)著作《周髀算經(jīng)》中，為了方便，在本題中，我們把三邊的比為3：4：5的三角形稱為（3，4，5）型三角形，例如：三邊長分別為9，12，15或的三角形就是（3，4，5）型三角形，用矩形紙片按下面的操作方法可以折出這種類型的三角形．32，42，52
實踐操作：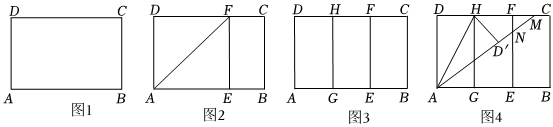
如圖1，在矩形紙片ABCD中，AD=8cm,AB=12cm.
第一步：如圖2，將圖1中的矩形紙片ABCD沿過點A的直線折疊，使點D落在AB上的點E處，折痕為AF，再沿EF折疊，然后把紙片展平．
第二步：如圖3，將圖2中的矩形紙片再次折疊，使點D與點F重合，折痕為GH，然后展平，隱去AF．
第三步：如圖4，將圖3中的矩形紙片沿AH折疊，得到△AD′H，再沿AD′折疊，折痕為AM，AM與折痕EF交于點N，然后展平．
問題解決：
（1）請在圖4中判斷NF與ND′的數(shù)量關(guān)系，并加以證明；
（2）請在圖4中證明△AEN（3，4，5）型三角形；
探索發(fā)現(xiàn)：
（3）在不添加字母的情況下，圖4中還有哪些三角形是（3，4，5）型三角形？請找出并直接寫出它們的名稱．發(fā)布：2025/5/25 2:0:6組卷：183引用：4難度：0.1 -
3．在數(shù)學(xué)興趣小組活動中，小亮進行數(shù)學(xué)探究活動．
（1）△ABC是邊長為3的等邊三角形，E是邊AC上的一點，且AE=1，小亮以BE為邊作等邊三角形BEF，如圖1．求CF的長；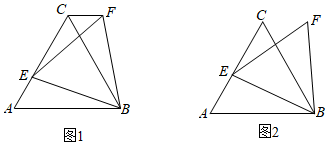
（2）△ABC是邊長為3的等邊三角形，E是邊AC上的一個動點，小亮以BE為邊作等邊三角形BEF，如圖2．在點E從點C到點A的運動過程中，求點F所經(jīng)過的路徑長；
（3）△ABC是邊長為3的等邊三角形，M是高CD上的一個動點，小亮以BM為邊作等邊三角形BMN，如圖3．在點M從點C到點D的運動過程中，求點N所經(jīng)過的路徑長；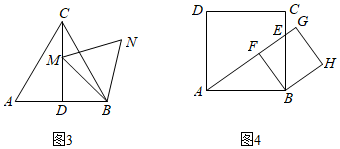
（4）正方形ABCD的邊長為3，E是邊CB上的一個動點，在點E從點C到點B的運動過程中，小亮以B為頂點作正方形BFGH，其中點F、G都在直線AE上，如圖4．當(dāng)點E到達點B時，點F、G、H與點B重合．則點H所經(jīng)過的路徑長為，點G所經(jīng)過的路徑長為．發(fā)布：2025/5/25 2:30:1組卷：3595引用：2難度：0.2