如圖，在△ABC中，∠B=90°，AB=8cm,BC=6cm,P，Q是△ABC邊上的兩個動點，其中點P從點A出發沿A→B方向向點B運動，速度為1cm/s,點Q從點B出發沿B→C方向向點C運動，速度為2cm/s,它們同時開始運動，其中一點停止時另一點也隨之停止運動．設運動的時間為t s.
（1）當t=2時，求PQ的長；
（2）當t為何值時，△PQB是等腰三角形？
（3）若點Q從點B出發沿B→C→A方向運動，則當點Q在邊CA上運動時，當t為何值時，△BCQ為等腰三角形？
【考點】三角形綜合題．
【答案】（1）PQ=cm；
（2）當時，△PQB是等腰三角形；
（3）t=5.5或6或6.6時，△BCQ為等腰三角形．
2
13
（2）當
t
=
8
3
（3）t=5.5或6或6.6時，△BCQ為等腰三角形．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：66引用：2難度：0.1
相似題
-
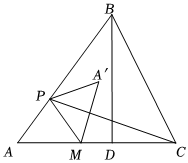1．在△ABC中，BD是AC邊上的高，AD=3，CD=2，BD=4，點M在AD上，且AM=2．動點P從點A出發，沿折線AB-BD以每秒1個單位長度的速度運動，連結PM，作點A關于直線PM的對稱點A′．設點P的運動時間為t秒（t＞0）．
（1）用含t的代數式表示線段BP的長；
（2）當點A′在△ABC內部時，求t的取值范圍；
（3）連結CP．當CP⊥AB時，求△BCP的面積；
（4）當MA′∥AB時，直接寫出t的值．發布：2025/6/9 21:30:1組卷：112引用：2難度：0.1 -
2．已知，點P為等邊三角形ABC所在平面內一點，且∠BPC=120°．
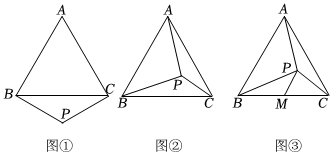
（1）如圖（1），∠ABP=90°，求證：BP=CP；
（2）如圖（2），點P在△ABC內部，且∠APB=90°，求證：BP=2CP；
（3）如圖（3），點P在△ABC內部，M為BC上一點，連接PM，若∠BPM+∠APC=180°，求證：BM=CM．發布：2025/6/9 21:30:1組卷：242引用：2難度：0.1 -
3．在平面直角坐標系中，有點A（a,0），B（0，b），且a,b滿足
+|b+2|=0，將線段AB向上平移k個單位得到線段CD．4-a
（1）直接寫出a=，b=；
（2）如圖1，點E為線段CD上任意一點，點F為線段AB上任意一點，∠EOF=120°．點G為線段AB與線段CD之間一點，連接GE，GF．且∠DEG=∠DEO，∠AFG=13∠AFO，求∠G的度數；13
（3）如圖2，若k=6，過點C作直線l∥x軸，點M為直線l上一點，延長BA交1于K
①用面積法求K點坐標；
②若△MAB的面積為10，求點M的坐標．發布：2025/6/9 20:30:1組卷：289引用：2難度：0.3