在四邊形ABCD中，AD∥BC，∠B=∠C=45°，AB=CD=3，AD=2．直角三角板含45°角的頂點(diǎn)E在BC上移動(dòng)，一直角邊始終經(jīng)過(guò)點(diǎn)A，斜邊與CD交于點(diǎn)F．
（1）如圖1，當(dāng)EC=3時(shí)，求證：△ABE≌△ECF；
（2）如圖2，在CD上有一點(diǎn)P，CP=2．若點(diǎn)E從點(diǎn)B到點(diǎn)C移動(dòng)的速度為每秒2個(gè)單位長(zhǎng)，求點(diǎn)P在直角三角板內(nèi)部（包括邊界）的時(shí)長(zhǎng)；
（3）連接AF，當(dāng)△AEF的外心落在△AEF的邊上時(shí)，求BE的值；
（4）直接寫出點(diǎn)E移動(dòng)過(guò)程中△ADF的外接圓半徑的最小值．
2
2
【考點(diǎn)】圓的綜合題．
【答案】（1）見解析；
（2）點(diǎn)P在直角三角板內(nèi)部（包括邊界）的時(shí)長(zhǎng)為2秒；
（3）BE的值或；
（4）點(diǎn)E移動(dòng)過(guò)程中△ADF的外接圓半徑的最小值為．
（2）點(diǎn)P在直角三角板內(nèi)部（包括邊界）的時(shí)長(zhǎng)為2秒；
（3）BE的值
2
5
2
2
（4）點(diǎn)E移動(dòng)過(guò)程中△ADF的外接圓半徑的最小值為
5
2
6
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：172引用：2難度：0.3
相似題
-
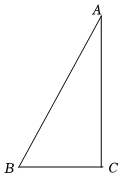1．如圖是小宇同學(xué)的錯(cuò)題積累本的部分內(nèi)容，請(qǐng)仔細(xì)閱讀，并完成相應(yīng)的任務(wù)．
任務(wù)：x年x月x日星期日
錯(cuò)題積累
在Rt△ABC中，∠C=90°，BD平分∠ABC交AC于點(diǎn)D，
O是AB上一點(diǎn)，且⊙O經(jīng)過(guò)B，D兩點(diǎn)，分別交AB，BC于
點(diǎn)E，F(xiàn)．
…
[自勉]
讀書使人頭腦充實(shí)，討論使人明辨是非，做筆記則能使知識(shí)精確．
——培根
（1）使用直尺和圓規(guī)，根據(jù)題目要求補(bǔ)全圖形（不寫作法，保留作圖痕跡）；
（2）求證：⊙O與AC相切于點(diǎn)D；
（3）若CD=，∠BDC=60°，則劣弧3的長(zhǎng)為 ．?ED發(fā)布：2025/5/24 1:30:2組卷：125引用：2難度：0.2 -
2．【問(wèn)題提出】如圖1，AB為⊙O的一條弦，點(diǎn)C在弦AB所對(duì)的優(yōu)弧上運(yùn)動(dòng)時(shí)，根據(jù)圓周角性質(zhì)，我們知道∠ACB的度數(shù)不變．愛動(dòng)腦筋的小芳猜想，如果平面內(nèi)線段AB的長(zhǎng)度已知，∠ACB的大小確定，那么點(diǎn)C是不是在某個(gè)確定的圓上運(yùn)動(dòng)呢？
【問(wèn)題探究】為了解決這個(gè)問(wèn)題，小芳先從一個(gè)特殊的例子開始研究．如圖2，若AB=4，線段AB上方一點(diǎn)C滿足∠ACB=45°，為了畫出點(diǎn)C所在的圓，小芳以AB為底邊構(gòu)造了一個(gè)Rt△AOB，再以點(diǎn)O為圓心，OA為半徑畫圓，則點(diǎn)C在⊙O上．后來(lái)小芳通過(guò)逆向思維及合情推理，得出一個(gè)一般性的結(jié)論．即：若線段AB的長(zhǎng)度已知，∠ACB的大小確定，則點(diǎn)C一定在某一個(gè)確定的圓上，即定弦定角必定圓，我們把這樣的幾何模型稱之為“定弦定角”模型．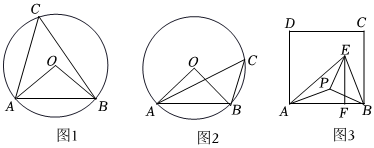
【模型應(yīng)用】
（1）若AB=6，平面內(nèi)一點(diǎn)C滿足∠ACB=60°，若點(diǎn)C所在圓的圓心為O，則∠AOB=，劣弧AB的長(zhǎng)為 ．
（2）如圖3，已知正方形ABCD以AB為腰向正方形內(nèi)部作等腰△ABE，其中AB=AE，過(guò)點(diǎn)E作EF⊥AB于點(diǎn)F，若點(diǎn)P是△AEF的內(nèi)心．
①求∠BPE的度數(shù)；
②連接CP，若正方形ABCD的邊長(zhǎng)為4，求CP的最小值．發(fā)布：2025/5/24 1:30:2組卷：547引用：3難度：0.5 -
3．（1）如圖1，⊙A的半徑為1，AB=2.5，點(diǎn)P為⊙A上任意一點(diǎn)，則BP的最小值為 ；
（2）如圖2，已知矩形ABCD，點(diǎn)E為AB上方一點(diǎn)，連接AE，BE，作EF⊥AB于點(diǎn)F，點(diǎn)P是△BEF的內(nèi)心，求∠BPE的度數(shù)；
（3）如圖3，在（2）的條件下，連接AP，CP，若矩形的邊長(zhǎng)AB=8，BC=4，BE=BA，求此時(shí)CP的最小值．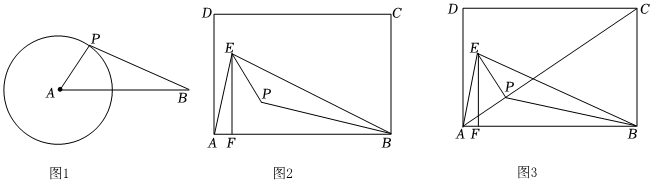
發(fā)布：2025/5/24 1:30:2組卷：206引用：1難度：0.3
相關(guān)試卷