綜合與探究
【閱讀理解】在一次數(shù)學(xué)活動(dòng)課上，張老師準(zhǔn)備了若干張如圖1所示的甲、乙、丙三種紙片，其中甲種紙片是邊長(zhǎng)為x的正方形，乙種紙片是邊長(zhǎng)為y的正方形，丙種紙片是長(zhǎng)為y,寬為x的長(zhǎng)方形，并用甲種紙片一張，乙種紙片一張，丙種紙片兩張拼成了如圖2所示的一個(gè)大正方形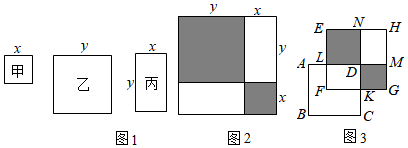
（1）①觀察圖2，用兩種不同方式表示陰影部分的面積可得到一個(gè)等式：（x+y）2=x2-2xy+y2（x+y）2=x2-2xy+y2．
②利用①中的等式解決問(wèn)題：若x+y=8，x2+y2=40，則xy的值為 1212．
【拓展探究】若x滿足（20-x）（x-30）=10，求（20-x）2+（x-30）2的值．
我們可以作如下解答：設(shè)a=20-x,b=x-30，
則（20-x）（x-30）=ab=10，a+b=（20-x）+（x-30）=20-30=-10，
所以（20-x）2+（x-30）2=a2+b2=（a+b）2-2ab=（-10）2-2×10=80．
（2）①若（4-x）x=5，則（4-x）2+x2=66．
②若（4-x）（5-x）=8，則（4-x）2+（5-x）2=1717．
【實(shí)際運(yùn)用】（3）如圖3，將正方形EFGH疊放在正方形ABCD上，重疊部分LFKD是一個(gè)長(zhǎng)方形，AL=8，CK=12．沿著LD、KD所在直線將正方形EFGH分割成四個(gè)部分，若四邊形ELDN和四邊形DKGM恰好為正方形，且它們的面積之和為400，求長(zhǎng)方形NDMH的面積．
【考點(diǎn)】完全平方公式的幾何背景；多項(xiàng)式乘多項(xiàng)式．
【答案】（x+y）2=x2-2xy+y2；12；6；17
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/7/11 8:0:9組卷：253引用：2難度：0.7
相似題
-
1．如圖（1），是一個(gè)長(zhǎng)為2a寬為2b（a＞b）的矩形，用剪刀沿矩形的兩條對(duì)角軸剪開(kāi)，把它分成四個(gè)全等的小矩形，然后按圖（2）拼成一個(gè)新的正方形，求中間空白部分的面積（用含a、b的式子表示）
發(fā)布：2025/6/18 10:0:1組卷：298引用：1難度：0.5 -
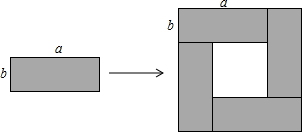2．如圖將4個(gè)長(zhǎng)、寬分別均為a,b的長(zhǎng)方形，擺成了一個(gè)大的正方形，利用面積的不同表示方法寫出一個(gè)代數(shù)恒等式是（ ）發(fā)布：2025/6/18 16:30:1組卷：5247引用：39難度：0.7 -
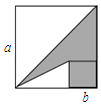3．如圖，兩個(gè)正方形邊長(zhǎng)分別為a、b,如果a+b=8，ab=13，則陰影部分的面積為．發(fā)布：2025/6/18 6:0:1組卷：1246引用：18難度：0.8