我國著名數學家華羅庚曾說過：“數缺形時少直觀，形少數時難入微；數形結合百般好，隔離分家萬事休”．數學中，數和形是兩個最主要的研究對象，它們之間有著十分密切的聯系，在一定條件下，數和形之間可以相互轉化，相互滲透．某校數學興趣小組，在學習完勾股定理和實數后，進行了如下的問題探索與分析．
【提出問題】已知0＜x＜1，求1+x2+1+（1-x）2的最小值．
【分析問題】由勾股定理，可以通過構造直角三角形的方法，來分別表示長度為 1+x2和1+（1-x）2的線段，將代數求和轉化為線段求和問題．
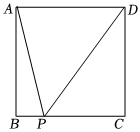
（1）如圖，我們可以構造邊長為1的正方形ABCD，P為BC邊上的動點．設BP=x,則
PC=1-x.則1+x2+1+（1-x）2的最小值等于 55．
?（2）運用以上數形結合的方法，求9+x2+1+（6-x）2的最小值；
（3）運用以上數形結合的方法，求x2+9-x2-12x+37的最大值．
1
+
x
2
+
1
+
（
1
-
x
）
2
1
+
x
2
1
+
（
1
-
x
）
2
1
+
x
2
+
1
+
（
1
-
x
）
2
5
5
9
+
x
2
+
1
+
（
6
-
x
）
2
x
2
+
9
-
x
2
-
12
x
+
37
【考點】四邊形綜合題．
【答案】
5
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/7/16 8:0:9組卷：325引用：1難度：0.5
相似題
-
1．（1）感知：如圖①，四邊形ABCD和CEFG均為正方形，BE與DG的數量關系為 ；
（2）拓展：如圖②，四邊形ABCD和CEFG均為菱形，且∠A=∠F，請判斷BE與DG的數量關系，并說明理由；
（3）應用：如圖③，四邊形ABCD和CEFG均為菱形，點E在邊AD上，點G在AD延長線上．若AE=2ED，∠A=∠F，△EBC的面積為8，求菱形CEFG的面積．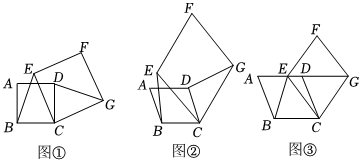
發布：2025/5/23 5:30:3組卷：229引用：1難度：0.3 -
2．如圖，在正方形ABCD中，，將正方形ABCD繞點C按順時針方向旋轉90°得到正方形CEFM．動點P從點A出發，沿AC方向運動，運動速度為1cm/s.過點P作AC的垂線，交AD于點Q，連接CQ，交PF于點H．設動點P的運動時間為t s（0＜t＜8）．解答下列問題：AB=42cm
?（1）當t為何值時，S△APQ：S△CDF=1：4？
（2）設△PFQ的面積為S cm2，求S與t之間的關系式；
（3）當運動時間為2 s時，求PH的長；
（4）若N是PF的中點，在運動的過程中，點N到∠DFE兩邊距離的和是否為定值？請說明理由．發布：2025/5/23 5:30:3組卷：264引用：1難度：0.1 -
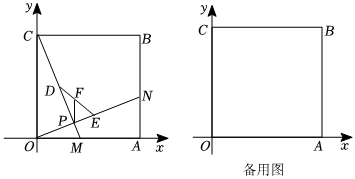3．如圖所示，在平面直角坐標系中，正方形OABC在第一象限，A（8，0）．點M，N分別為邊OA，AB上的動點，且點OM=AN，D，E分別為CM，ON的中點，F是DE的中點．設OM=t,點P的縱坐標為y,請解決下列問題：
（1）判斷CM與ON的位置關系，并寫出證明過程；
（2）請求出y關于t的函數表達式，并直接寫出y最大時，點P的坐標；
（3）在點M從點O運動到點A的過程中，設點F走過的路線長為L，線段PF掃過的面積為S，請直接寫出L與S的值．發布：2025/5/23 6:0:2組卷：77引用：1難度：0.3