當(dāng)前位置：試卷中心 > 試卷詳情

2022-2023學(xué)年江蘇省揚(yáng)州市梅嶺教育集團(tuán)八年級（下）期中數(shù)學(xué)試卷

發(fā)布：2024/7/16 8:0:9

一、選擇題（本大題共8小題，每小題3分，共24分，每小題僅有一個答案正確，請把你認(rèn)為正確的答案填寫在答題紙相應(yīng)位置。）

1．下列圖形中，既是軸對稱圖形，又是中心對稱圖形的是（　　）
A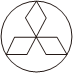． B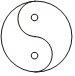． C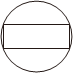． D．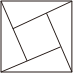
組卷：40引用：1難度：0.9
解析
2．下列代數(shù)式中，屬于分式的是（　　）
A．
x
-
2
3
B．
x
π
C．
2
x
+
3
D．
1
2
組卷：96引用：2難度：0.8
解析
3．下列是最簡二次根式的是（　　）
A．
1
3
B．
9
C．
1
5
D．
2
組卷：154引用：2難度：0.5
解析
4．若分式
x
+
y
3
xy
中的x和y都擴(kuò)大3倍，那么分式的值（　　）
A．?dāng)U大3倍 B．不變 C．縮小9倍 D．縮小3倍
組卷：386引用：3難度：0.5
解析
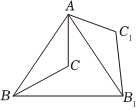5．如圖，△ABC繞點A按逆時針方向旋轉(zhuǎn)68°后與△AB₁C₁重合，連接BB₁，則∠ABB₁=（　　）
A．56° B．58° C．62° D．68°
組卷：305引用：5難度：0.5
解析
6．估計
（
12
+
6
）
÷
3
的值應(yīng)在（　　）
A．2和3之間 B．3和4之間 C．4和5之間 D．5和6之間
組卷：108引用：5難度：0.7
解析
7．化簡
（
1
-
a
）
1
a
-
1
的結(jié)果是（　　）
A．
1
-
a
B．
-
a
-
1
C．
-
1
-
a
D．
a
-
1
組卷：678引用：4難度：0.6
解析
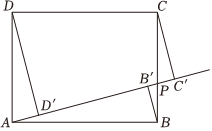8．如圖，已知矩形ABCD中，AB=4，AD=3．點P為BC上任意一點（可與點B或C重合），分別過B、C、D作射線AP的垂線，垂足分別是B′、C′、D′，則BB′+CC′+DD′的最小值是（　　）
A．5 B．
12
5
C．
24
5
D．
12
5
5
組卷：409引用：1難度：0.5
解析

二.填空題（本大題共10小題，每小題3分，共30分，請把你認(rèn)為正確的答案填寫在答題紙相應(yīng)位置。）

9．在函數(shù)
y
=
x
-
3
x
-
4
中，自變量x的取值范圍是

．
組卷：495引用：38難度：0.9
解析

當(dāng)前模式為游客模式，立即登錄查看試卷全部內(nèi)容及下載

三、解答題（本大題共10小題，共96分，解答應(yīng)寫出必要的文字說明、證明過程或演算步驟，請把答案填寫在答題紙相應(yīng)位置。）

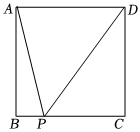27．我國著名數(shù)學(xué)家華羅庚曾說過：“數(shù)缺形時少直觀，形少數(shù)時難入微；數(shù)形結(jié)合百般好，隔離分家萬事休”．?dāng)?shù)學(xué)中，數(shù)和形是兩個最主要的研究對象，它們之間有著十分密切的聯(lián)系，在一定條件下，數(shù)和形之間可以相互轉(zhuǎn)化，相互滲透．某校數(shù)學(xué)興趣小組，在學(xué)習(xí)完勾股定理和實數(shù)后，進(jìn)行了如下的問題探索與分析．
【提出問題】已知0＜x＜1，求
1
+
x
2
+
1
+
（
1
-
x
）
2
的最小值．
【分析問題】由勾股定理，可以通過構(gòu)造直角三角形的方法，來分別表示長度為
1
+
x
2
和
1
+
（
1
-
x
）
2
的線段，將代數(shù)求和轉(zhuǎn)化為線段求和問題．
（1）如圖，我們可以構(gòu)造邊長為1的正方形ABCD，P為BC邊上的動點．設(shè)BP=x,則
PC=1-x.則
1
+
x
2
+
1
+
（
1
-
x
）
2
的最小值等于
．
?（2）運(yùn)用以上數(shù)形結(jié)合的方法，求
9
+
x
2
+
1
+
（
6
-
x
）
2
的最小值；
（3）運(yùn)用以上數(shù)形結(jié)合的方法，求
x
2
+
9
-
x
2
-
12
x
+
37
的最大值．
組卷：325引用：1難度：0.5
解析
28．實踐操作
在矩形ABCD中，AB=4，AD=3，現(xiàn)將紙片折疊，點D的對應(yīng)點記為點P，折痕為EF（點E、F是折痕與矩形的邊的交點），再將紙片還原．
初步思考
（1）若點P落在矩形ABCD的邊AB上（如圖①）．
當(dāng)點P與點A重合時，∠DEF=
°；當(dāng)點E與點A重合時，∠DEF=
°；
深入探究
（2）當(dāng)點E在AB上，點F在DC上時（如圖②），求證：四邊形DEPF為菱形，并直接寫出當(dāng)
AP
=
7
2
時的菱形EPFD的邊長．
拓展延伸
（3）若點F與點C重合，點E在AD上，射線BA與射線FP交于點M（如圖③）．在折疊過程中，是否存在使得線段AM與線段DE的長度相等的情況？若存在，請求出線段AE的長度；若不存在，請說明理由．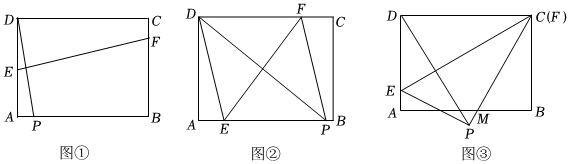
組卷：2022引用：13難度：0.5
解析