公元3世紀，古希臘數(shù)學家丟番圖（Diophantus）在其《算術》一書中設置了以下問題：已知兩正整數(shù)之和為20，乘積為96，求這兩個數(shù)．因為兩數(shù)之和為20，所以這兩個數(shù)不可能同時大于10，也不可能同時小于10，必定是一個大于10，一個小于10．根據(jù)如圖所示的設法，可設一個數(shù)為10+x,則另一個數(shù)為10-x,根據(jù)兩數(shù)之積為96，可得（10+x）（10-x）=96．
請根據(jù)以上思路解決下列問題：
（1）若兩個正整數(shù)之和為100，大數(shù)比小數(shù)大2a,根據(jù)丟番圖的設法，這兩個正整數(shù)可表示為 （50+a）（50+a）和 （50-a）（50-a）．
（2）請你根據(jù)丟番圖的運算方法，計算502×498的值．
【考點】列代數(shù)式；有理數(shù)的混合運算．
【答案】（50+a）；（50-a）
【解答】
【點評】
聲明：本試題解析著作權屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復制發(fā)布。
發(fā)布：2025/6/10 6:0:2組卷：60引用：1難度：0.7
相似題
-
1．材料一：對于一個三位正整數(shù)，若百位數(shù)字與個位數(shù)字之和減去十位數(shù)字的差為3，則稱這個三位數(shù)為“尚美數(shù)”，例如：234，因為2+4-3=3，所以234是“尚美數(shù)”；
材料二：若t=（1≤a≤9，0≤b≤9，0≤c≤9且a、b、c均為整數(shù)），記F（t）=2a-c.abc
（1）345 “尚美數(shù)”（填“是”或“不是”）；若是“尚美數(shù)”，且2bc，則b的值為 ；F（2bc）=-1
（2）已知t1=，t2=2yz是兩個不同的“尚美數(shù)”（0≤y≤8，0≤n≤9，1≤m、z≤9且y、z、m、n均為整數(shù)），且F（t1）+2F（t2）+4n能被13整除，求所有符合題意的t1的值．myn發(fā)布：2025/6/13 5:30:2組卷：289引用：3難度：0.6 -
2．小明房間窗戶的裝飾物如圖所示，它們由三個半圓組成（它們的半徑相同）．解答下列問題（結果保留π）
（1）用代數(shù)式表示裝飾物所占的面積是．
（2）用代數(shù)式表示窗戶中能射進陽光部分面積是．（窗框面積忽略不計）
（3）若a=3，b=2，則窗戶中部分能射進陽光的面積是．發(fā)布：2025/6/13 10:0:1組卷：350引用：7難度：0.6 -
3．觀察下列每對數(shù)在數(shù)軸上的對應點間的距離，3與5，4與-2，-4與3，-1與-5．并回答下列各題：
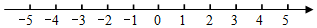
（1）數(shù)軸上表示4和-2兩點間的距離是；表示-1和-5兩點間的距離是．
（2）若數(shù)軸上的點A表示的數(shù)為x,點B表示的數(shù)為-3．
①數(shù)軸上A、B兩點間的距離可以表示為（用含x的代數(shù)式表示）；
②如果數(shù)軸上A、B兩點間的距離為|AB|=1，求x的值．
（3）直接寫出代數(shù)式|x+2|+|x-3|的最小值為．發(fā)布：2025/6/13 5:30:2組卷：169引用：4難度：0.6