如圖是東寶塔，它是荊門市現存的唯一一處具有千年歷史的地面文物．建于隋開皇十三年（公元593年），位于東寶山山頂．寶塔七層四面八角，隔面設窗，攢尖式塔頂，巍然獨秀，直透蒼穹．其集風水寶塔與紀念塔為一身，是東寶山風景區的主體建筑．寶塔建造工藝精湛，與鐘祥龍山的文峰塔遙相呼應．某數學興趣小組開展了測量“東寶塔的高度”的實踐活動，具體過程如下：
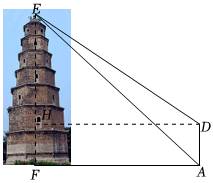
方案設計：如圖，寶塔EF垂直于地面，在地面上選取A處測得∠EAF的度數（點A，F在同一直線上）；接著在點A的正上方搭高度為5米的平臺，在D處測得∠EDH的度數．
數據收集：通過實地測量：∠EAF=43°，∠EDH=36°．
問題解決：求寶塔EF的高度和地面A點與塔底F點之間的距離（結果精確到0.1m）．
（參考數據：sin36°≈0.59，cos36°≈0.81，tan36°≈0.73，sin43°≈0.68，cos43°≈0.73，tan43°≈0.93）．
【考點】解直角三角形的應用．
【答案】寶塔EF的高度約是23，3m，地面A點與塔底F點之間的距離約是25m．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/5/24 2:0:8組卷：97引用：1難度：0.5
相似題
-
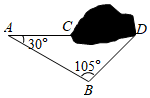1．某高鐵路段修建過程中需要經過一座小山．如圖，施工方計劃沿AC方向開挖隧道，為了加快施工速度，要在小山的另一側D處（A、C、D共線）同時施工．測得∠CAB=30°，AB=4km,∠ABD=105°，則BD的長為．（結果保留根號）發布：2025/5/25 1:0:1組卷：430引用：3難度：0.5 -
2．圖1是一個地鐵站入口的雙翼閘機．如圖2，當雙翼收起時，可以通過閘機的物體的最大寬度是64cm,它的雙翼展開時，雙翼邊緣的端點A與B之間的距離為10cm.此時雙翼的邊緣AC、BD與閘機側立面夾角∠PCA=∠BDQ=30°，則雙翼的邊緣AC、BD（AC=BD）的長度為（ ）
發布：2025/5/25 0:30:1組卷：486引用：3難度：0.7 -
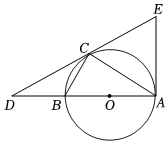3．古希臘數學家畢達哥拉斯認為：“一切平面圖形中最美的是圓”，請研究如下美麗的圓，如圖，以O為圓心，AB長為直徑作圓，在⊙O上取一點C，延長AB至點D，連接DC、AC、BC，過點A作⊙O的切線交DC的延長線于點E，且∠DCB=∠DAC．
（1）求證：CD是⊙O的切線；
（2）若AD=6，tan∠DCB=，則：23
①求CD的長；
②求CE的長．發布：2025/5/25 0:30:1組卷：560引用：3難度：0.5