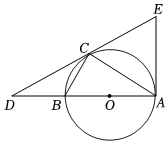
古希臘數學家畢達哥拉斯認為：“一切平面圖形中最美的是圓”，請研究如下美麗的圓，如圖，以O為圓心，AB長為直徑作圓，在⊙O上取一點C，延長AB至點D，連接DC、AC、BC，過點A作⊙O的切線交DC的延長線于點E，且∠DCB=∠DAC．
（1）求證：CD是⊙O的切線；
（2）若AD=6，tan∠DCB=23，則：
①求CD的長；
②求CE的長．
2
3
【答案】（1）證明見解答過程；
（2）①4；
②．
（2）①4；
②
5
2
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/4/20 14:35:0組卷：560引用：3難度：0.5
相似題
-
1．圖1是一種可調節桌面畫架，畫架側面及相關數據如圖2所示．B是底座OA上一固定支點，點C在滑槽DE內滑動，支桿BC長度不變．已知DE=24cm,當C從點D出發滑向終點E，∠AOF從0°逐漸增大至90°，則支桿BC的長為 cm,若點F到OA的距離為40cm,則EC=cm.發布：2025/5/23 2:0:6組卷：305引用：3難度：0.6 -
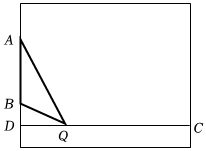2．備受矚目的卡塔爾世界杯掀起了全民足球運動的熱潮．如圖為某中學的矩形足球場的一部分，點A、B為球門邊框（不考慮球門的高度）的兩個端點，AB=6米，CD⊥AB于點D．某學生沿CD向球門AB進攻，在Q點起腳射門，此時射門角∠AQB=36°，∠QAB=27°．求射門點Q到球門AB的距離QD的長度．（結果保留整數）（參考數據：sin27°≈0.45，cos27°≈0.90，tan27°≈0.51，sin36°≈0.59，cos36°≈0.81，tan36°≈0.73）發布：2025/5/23 0:0:1組卷：126引用：3難度：0.6 -
3．第24屆冬季奧林匹克運動會于今年2月4日至20日在北京舉行，我國冬奧選手取得了9塊金牌、4塊銀牌、2塊銅牌，為祖國贏得了榮譽，激起了國人對冰雪運動的熱情．某地模仿北京首鋼大跳臺建了一個滑雪大跳臺（如圖1），它由助滑坡道、弧形跳臺、著陸坡、終點區四部分組成．圖2是其示意圖，已知：助滑坡道AF=50米，弧形跳臺的跨度FG=7米，頂端E到BD的距離為40米，HG∥BC，∠AFH=40°，∠EFG=25°，∠ECB=36°．求此大跳臺最高點A距地面BD的距離是多少米（結果保留整數）．
（參考數據：sin40°≈0.64，cos40°≈0.77，tan40°≈0.84，sin25°≈0.42，cos25°≈0.91，tan25°≈0.47，sin36°≈0.59，cos36°≈0.81，tan36°≈0.73）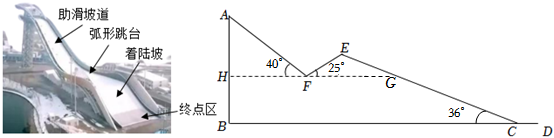
發布：2025/5/23 1:30:2組卷：1446引用：6難度：0.5