綜合與實踐
綜合實踐課上，老師讓同學們以“三角形紙片的折疊”為主題開展數學活動．
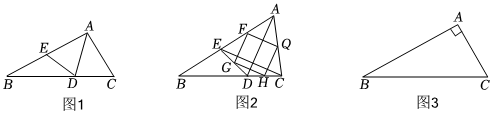
（1）【操作發現】對折△ABC（AB＞AC），使點C落在邊AB上的點E處，得到折痕AD，把紙片展平，如圖1．小明發現四邊形AEDC滿足：AE=AC，DE=DC．查閱相關資料得知，像這樣的有兩組鄰邊分別相等的四邊形叫作“箏形”．請寫出圖1中箏形AEDC的一條性質：答案不唯一，以下任意一條均可，
①箏形AEDC是軸對稱圖形，對稱軸是直線AD；
②箏形的兩條對角線互相垂直；
③箏形的對角線AD平分一組對角；
④箏形的對角線AD是對角線EC的垂直平分線答案不唯一，以下任意一條均可，
①箏形AEDC是軸對稱圖形，對稱軸是直線AD；
②箏形的兩條對角線互相垂直；
③箏形的對角線AD平分一組對角；
④箏形的對角線AD是對角線EC的垂直平分線．
（2）【拓展探究】如圖2，連接EC，F、G、H、Q分別為AE、ED、DC、AC的中點．
①求證：箏形AEDC的面積S=12AD?EC；
②若△ABC的面積為64，△BED的面積為12，求四邊形FGHQ的面積．
（3）【遷移應用】如圖3，在Rt△ABC中，∠A=90°，∠B=30°，點D、E分別在BC、AB上，當四邊形AEDC是箏形，AD=6時，直接寫出四邊形AEDC的面積．
?
①箏形AEDC是軸對稱圖形，對稱軸是直線AD；
②箏形的兩條對角線互相垂直；
③箏形的對角線AD平分一組對角；
④箏形的對角線AD是對角線EC的垂直平分線
①箏形AEDC是軸對稱圖形，對稱軸是直線AD；
②箏形的兩條對角線互相垂直；
③箏形的對角線AD平分一組對角；
④箏形的對角線AD是對角線EC的垂直平分線
S
=
1
2
AD
?
EC
6
【考點】四邊形綜合題．
【答案】答案不唯一，以下任意一條均可，
①箏形AEDC是軸對稱圖形，對稱軸是直線AD；
②箏形的兩條對角線互相垂直；
③箏形的對角線AD平分一組對角；
④箏形的對角線AD是對角線EC的垂直平分線
①箏形AEDC是軸對稱圖形，對稱軸是直線AD；
②箏形的兩條對角線互相垂直；
③箏形的對角線AD平分一組對角；
④箏形的對角線AD是對角線EC的垂直平分線
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/7/3 8:0:9組卷：127引用：2難度：0.1
相似題
-
1．在△ABC中，AB=AC，點D為AB邊上一動點，∠CDE=∠BAC=α，CD=ED，連接BE，EC．
（1）問題發現：
如圖①，若α=60°，則∠EBA=，AD與EB的數量關系是 ；
（2）類比探究：
如圖②，當α=90°時，請寫出∠EBA的度數及AD與EB的數量關系并說明理由；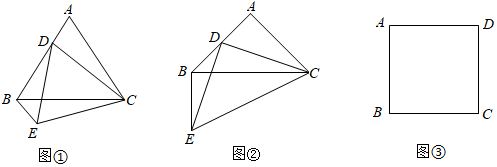
（3）拓展應用：
如圖③，點E為正方形ABCD的邊AB上的三等分點，以DE為邊在DE上方作正方形DEFG，點O為正方形DEFG的中心，若OA=，請直接寫出線段EF的長度．2發布：2025/5/25 1:30:1組卷：780引用：3難度：0.3 -
2．在Rt△ABC中，∠ACB=90°，∠A=60°，AC=2．點P為線段AB（不與點A和點B重合）上一點，連接CP，將△ACP沿CP翻折得到△DCP．
（1）如圖1，當點D落在AB上時，AP=；
（2）如圖2，當DP∥AC時，判斷四邊形ACDP的形狀，并說明理由；
（3）當點D落在△ABC內部時，直接寫出AP的取值范圍．發布：2025/5/25 1:30:1組卷：70引用：1難度：0.2 -
3．背景閱讀：
早在三千多年前，我國周朝數學家商高就提出：將一根直尺折成一個直角，如果勾等于三，股等于四，那么弦就等于五，即“勾三、股四、弦五”．它被記載與我國古代著名數學著作《周髀算經》中，為了方便，在本題中，我們把三邊的比為3：4：5的三角形稱為（3，4，5）型三角形，例如：三邊長分別為9，12，15或的三角形就是（3，4，5）型三角形，用矩形紙片按下面的操作方法可以折出這種類型的三角形．32，42，52
實踐操作：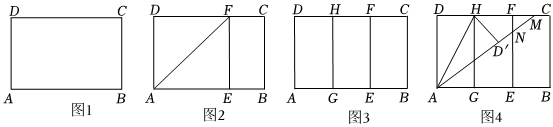
如圖1，在矩形紙片ABCD中，AD=8cm,AB=12cm.
第一步：如圖2，將圖1中的矩形紙片ABCD沿過點A的直線折疊，使點D落在AB上的點E處，折痕為AF，再沿EF折疊，然后把紙片展平．
第二步：如圖3，將圖2中的矩形紙片再次折疊，使點D與點F重合，折痕為GH，然后展平，隱去AF．
第三步：如圖4，將圖3中的矩形紙片沿AH折疊，得到△AD′H，再沿AD′折疊，折痕為AM，AM與折痕EF交于點N，然后展平．
問題解決：
（1）請在圖4中判斷NF與ND′的數量關系，并加以證明；
（2）請在圖4中證明△AEN（3，4，5）型三角形；
探索發現：
（3）在不添加字母的情況下，圖4中還有哪些三角形是（3，4，5）型三角形？請找出并直接寫出它們的名稱．發布：2025/5/25 2:0:6組卷：183引用：4難度：0.1