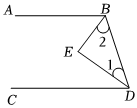
如圖，已知：BE平分∠ABD，DE平分∠BDC，且∠1=30°，∠2=2∠1．
（1）試判斷AB與CD的位置關系，并說明理由；
（2）求證：BE⊥DE．
【考點】平行線的判定與性質．
【答案】（1）AB∥CD，理由見解答過程；
（2）證明見解答過程．
（2）證明見解答過程．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：258引用：3難度：0.6
相似題
-
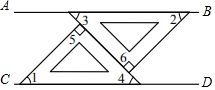1．如圖，小明用兩塊同樣的三角板，按下面的方法作出了平行線，則AB∥CD的理由是（ ）發布：2025/6/3 19:0:1組卷：877引用：9難度：0.4 -
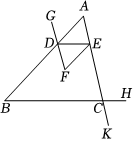2．完成下面的證明．
如圖，∠GDB+∠F=180°，∠DEF=∠B．判斷∠AED與∠HCK的數量關系，并證明．
結論：∠AED=∠HCK．
證明：∵∠GDB+∠BDF=180°（ ），
∠GDB+∠F=180°（已知），
∴∠F=∠BDF（ ），
∴EF∥AB（ ），
∴∠DEF=∠ADE（ ），
∵∠DEF=∠B（已知），
∴∠B=（等量代換）．
∴DE∥BC（ ），
∴∠AED=∠ACB（ ），
∵∠ACB=∠HCK（ ），
∴∠AED=∠HCK（等量代換）．發布：2025/6/3 19:0:1組卷：156引用：1難度：0.7 -
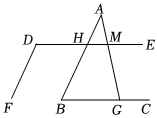3．如圖，已知直線AB∥DF，∠D+∠B=180°．
（1）求證：DE∥BC；
（2）如果∠AMD=70°，求∠AGC的度數．發布：2025/6/3 18:0:1組卷：901引用：2難度：0.5