如圖，在△ABC中，∠A=30°，∠B=45°，AC=22．
（1）求AB的長；
（2）用尺規作三角形ABC的外接圓（不寫作法，保留作圖痕跡），并求此外接圓的半徑．
2
【答案】（1）．
（2）畫圖見解答；2．
6
+
2
（2）畫圖見解答；2．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/5/23 5:0:2組卷：198引用：2難度：0.5
相似題
-
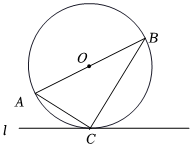1．如圖，Rt△ABC內接于⊙O，∠ACB=90°，直線l與⊙O相切于點C．
（1）用無刻度的直尺和圓規作圖：過點O作射線OD∥AC，交直線l于點D．（要求：不寫作法，保留作圖痕跡）
（2）在（1）的基礎上，若AB=10，BC=8，求CD的長．發布：2025/5/24 6:0:2組卷：83引用：1難度：0.6 -
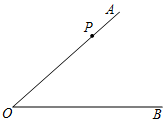2．如圖，點P是∠AOB邊OA上的一點，按要求作（畫）圖，并填空：
（1）用圓規和直尺作線段OP的垂直平分線，交OA、OB分別于點M、N；
（2）過點M畫出表示點M到直線OB距離的線段MH；
（3）點N到直線OB的距離的大小為；發布：2025/5/24 5:0:1組卷：63引用：3難度：0.7 -
3．已知：線段AB．
求作：Rt△ABC，使得∠BAC=90°，∠C=30°．
作法：
①分別以點A和點B為圓心，AB長為半徑作弧，兩弧交于點D；
②連接BD，在BD的延長線上截取DC=BD；
③連接AC．
則△ABC為所求作的三角形．
（1）使用直尺和圓規，依作法補全圖形（保留作圖痕跡）；
（2）完成下面的證明．
證明：連接AD．
∵AB=AD=BD，
∴△ABD為等邊三角形（ ）．（填推理的依據）
∴∠B=∠ADB=60°．
∵CD=BD，
∴AD=CD
∴∠DAC=（ ）．（填推理的依據）
∴∠ADB=∠C+∠DAC=60°．
∴∠C=30°．
在△ABC中，
∠BAC=180°-（∠B+∠C）=90°．發布：2025/5/24 4:30:1組卷：206引用：6難度：0.5