閱讀理解：配方法是中學(xué)數(shù)學(xué)的重要方法，用配方法可求最大（小）值．
對于任意正實(shí)數(shù)a、b,可作如下變形：a+b=（a）2+（b）2=（a）2+（b）2-2 ab+2ab=（a-b）2+2ab，
又∵（a-b）2≥0，∴（a-b）2+2ab≥0+2ab，即a+b≥2ab．
根據(jù)上述內(nèi)容，回答下列問題：在a+b≥2ab（a、b均為正實(shí)數(shù)）中，若ab為定值p,則a+b≥2p，當(dāng)且僅當(dāng)a、b滿足a=ba=b時(shí)，a+b有最小值2p．
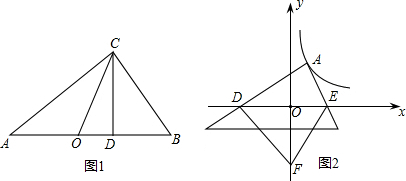
（2）思考驗(yàn)證：如圖1，△ABC中，∠ACB=90°，CD⊥AB，垂足為D，CO為AB邊上中線，AD=2a,DB=2b,試根據(jù)圖形驗(yàn)證a+b≥2ab成立，并指出等號成立時(shí)的條件．
（3）探索應(yīng)用：如圖2，已知A為反比例函數(shù)y=4x的圖象上一點(diǎn)，A點(diǎn)的橫坐標(biāo)為1，將一塊三角板的直角頂點(diǎn)放在A處旋轉(zhuǎn)，保持兩直角邊始終與x軸交于兩點(diǎn)D、E，F(xiàn)（0，-3）為y軸上一點(diǎn)，連接DF、EF，求四邊形ADFE面積的最小值．
a
b
a
b
ab
ab
a
b
ab
a
b
a
b
ab
ab
ab
ab
p
p
ab
4
x
【考點(diǎn)】反比例函數(shù)綜合題．
【答案】a=b
【解答】
【點(diǎn)評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：293引用：4難度：0.1
相似題
-
1．探究：是否存在一個(gè)新矩形，使其周長和面積為原矩形的2倍、倍、k倍．12
（1）若該矩形為正方形，是否存在一個(gè)正方形，使其周長和面積都為邊長為2的正方形的2倍？（填“存在”或“不存在”）．
（2）繼續(xù)探究，是否存在一個(gè)矩形，使其周長和面積都為長為3，寬為2的矩形的2倍？
同學(xué)們有以下思路：
①設(shè)新矩形長和寬為x、y,則依題意x+y=10，xy=12，聯(lián)立得x2-10x+12=0，再探究根的情況；x+y=10xy=12
根據(jù)此方法，請你探究是否存在一個(gè)矩形，使其周長和面積都為原矩形的倍；12
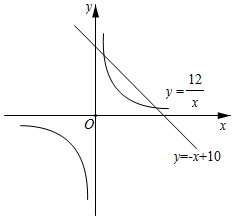
②如圖也可用反比例函數(shù)與一次函數(shù)證明l1：y=-x+10，l2：y=，那么，12x
a.是否存在一個(gè)新矩形為原矩形周長和面積的2倍？．
b.請?zhí)骄渴欠裼幸恍戮匦沃荛L和面積為原矩形的，若不存在，用圖象表達(dá)；12
c.請直接寫出當(dāng)結(jié)論成立時(shí)k的取值范圍：．發(fā)布：2025/5/25 12:0:2組卷：4070引用：4難度：0.3 -
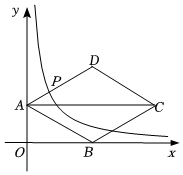2．如圖，菱形ABCD在第一象限，點(diǎn)A、B分別在y軸、x軸上，對角線AC∥x軸，點(diǎn)C（12，3），反比例函數(shù)y=（x＞0）的圖象交邊AD于點(diǎn)P，且AP：PD=1：2．kx
（1）求k的值．
（2）將菱形ABCD沿y軸向下平移m個(gè)單位，當(dāng)點(diǎn)D落在反比例函數(shù)y=（x＞0）的圖象時(shí)，求菱形ABCD平移所掃過的面積．kx發(fā)布：2025/5/25 8:30:2組卷：93引用：1難度：0.4 -
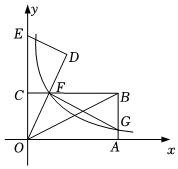3．如圖，在平面直角坐標(biāo)系中，矩形OABC的頂點(diǎn)B的坐標(biāo)為（4，2），OA，OC分別落在x軸和y軸上，OB是矩形的對角線，將△OAB繞點(diǎn)O逆時(shí)針旋轉(zhuǎn)，使點(diǎn)B落在y軸上，得到△ODE，OD與CB相交于點(diǎn)F，反比例函數(shù)y=（x＞0）的圖象經(jīng)過點(diǎn)F，交AB于點(diǎn)G．kx
（1）求tan∠COF的值及反比例函數(shù)表達(dá)式．
（2）在x軸上是否存在一點(diǎn)M，使|MF-MG|的值最大？若存在，求出點(diǎn)M；若不存在，說明理由．
（3）在線段OA上存在這樣的點(diǎn)P，使得△PFG是等腰三角形，請直接寫出OP的長．發(fā)布：2025/5/25 11:30:2組卷：468引用：1難度：0.4