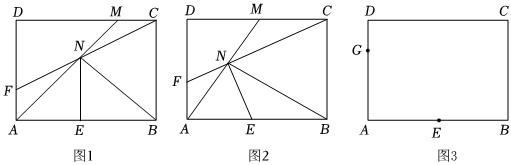
如圖1，矩形ABCD中，AB=4，AD=3，點E為AB的中點，點M為射線DC上一個動點，連接AM，以點E為圓心，以AE的長為半徑作弧，交AM于點N，連接BN，作射線CN交AD于點F．
（1）判斷：∠ANB的度數為 9090°；
（2）如圖2，當點M為CD的中點時，判斷線段NF與線段AF的數量關系并說明理由；
（3）如圖3，點G為AD上一點，且DG=1，當∠CNG=90° 時，直接寫出DM的長．
【考點】四邊形綜合題．
【答案】90
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：41引用：1難度：0.2
相似題
-
1．已知，四邊形ABCD為菱形，點E、F、M分別為邊AD、AB、CD上的點，連接CF、ME相交于點G，滿足∠ABC+∠CGE=180°．
（1）如圖1，若∠ABC=90°，求證：EM=CF；
（2）如圖2，若∠ABC≠90°，（1）中結論是否成立？請說明理由；
（3）如圖3，在（1）的條件下，若∠DCF=15°，點G為CF的中點，BE=，連接BD交MN于點H，則HG的長度為 ．（請直接寫出答案）2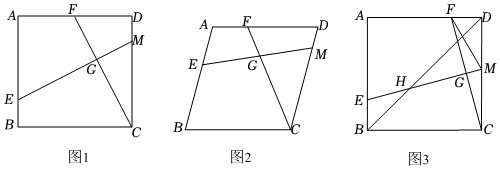
發布：2025/6/12 9:30:1組卷：89引用：1難度：0.2 -
2．如圖，已知正方形ABCD的邊長為2，E是邊BC上的動點，BF⊥AE交CD于點F，垂足為G，連接CG．下列說法：①AG＞GE；②AE=BF；③點G運動的路徑長為π；④CG的最小值為-1．其中正確的說法是．（把你認為正確的說法的序號都填上）5發布：2025/6/12 5:0:1組卷：2795引用：11難度：0.7 -
3．為了解決一些較為復雜的數學問題，我們常常采用從特殊到一般的思想，先從特殊的情形入手，從中找到解決問題的方法．
已知：在四邊形ABCD中，AC平分∠BAD，∠B+∠D=180°．
（1）如圖①，當∠B=90°時，求證：CB=CD；
（2）如圖②，當∠B＜90°時，
①求證：CB=CD；
②若AB=10cm,AD=6cm,∠B=45°，則點C到AB的距離是 cm.
發布：2025/6/12 4:30:1組卷：367引用：3難度：0.4