2022-2023學年河南省平頂山市寶豐縣紅星學校等五校九年級（下）月考數學試卷（3月份）

一、選擇題（每小題3分，共30分）下列各小題均有四個選項，其中只有一個是正確的，將正確選項的代號字母填入題后括號內．

• 1．下列四個數中，最小的數是（　　）

  A．0

  B．-3

  C．-π

  D．- 3
  組卷：46引用：3難度：0.8

  解析

• 2．2022年女籃世界杯錦標賽于9月22日至10月1日在澳大利亞舉行，本屆世界杯中國女籃發揮出色，時隔28年再次收獲國際大賽亞軍．據數據統計，世界杯女籃決賽吸引1800萬中國觀眾通過電視觀看，另有2300萬人通過網絡直播的方式觀看決賽．其中數據“2300萬”用科學記數法表示為（　　）

  A．2.3×107

  B．2.3×108

  C．0.23×108

  D．0.23×109
  組卷：62引用：2難度：0.8

  解析

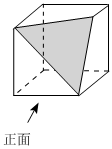• 3．如圖是切去一個角的正方體模具，則它的左視圖為（　　）

  A．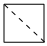

  B．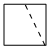

  C．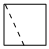

  D．
  組卷：67引用：1難度：0.8

  解析

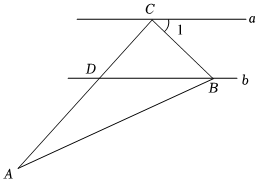• 4．如圖，直線a∥b,將一個直角三角形紙片如圖放置，∠ACB=90°，∠A=22°，點C落在直線a上，點B落在直線b上，且AC交直線b于點D，若AD=BD，則∠1的度數為（　　）

  A．44°

  B．46°

  C．48°

  D．52°
  組卷：103引用：1難度：0.7

  解析

• 5．下列運算正確的是（　　）

  A．a6÷a3=a2	B．（a+b）（a-b）=a2-b2
  C．（-a3）3=-a6	D．2a2+3a3=5a5
  組卷：107引用：2難度：0.8

  解析

• 6．下列條件中，菱形具有而矩形不具有的是（　　）

  A．對邊相等	B．對角線互相平分
  C．對角線相等	D．對角線互相垂直
  組卷：330引用：9難度：0.9

  解析

• 7．滿足不等式組

  2 x ≤ 1

  x + 2 ＞ 1

  的整數解是（　　）

  A．-2

  B．-1

  C．0

  D．1
  組卷：268引用：1難度：0.8

  解析

三、解答題（本大題共8個小題，滿分75分）

• 22．請閱讀下列材料，完成相應的任務：
  羅狄斯托勒密（Claudius Ptolemaeus,約90年168年），“地心說”的集大成者，生于埃及，著名的天文學家，地理學家、占星學家和光學家．
  托勒密定理實出自依巴谷（Hipparchus）之手，托勒密從他的書中摘出并加以完善．
  托勒密定理：圓的內接四邊形兩對對邊乘積的和等于兩條對角線的乘積．
  如圖1，四邊形ABCD內接于⊙O，求證：AB?CD+BC?AD=AC?BD
  下面是該結論的證明過程：
  證明：如圖1，作∠BAE=∠CAD，交BD于點E．∵

  ?

  AD

  =

  ?

  AD

  ，∴∠ABE=∠ACD（依據1），∴△ABE∽△ACD（依據2），∴

  AB

  AC

  =

  BE

  CD

  ，∴AB?CD=AC?BE，∵

  ?

  AB

  =

  ?

  AB

  ，∴∠ACB=∠ADE，∵∠BAE=∠CAD，∴∠BAE+∠EAC=∠CAD+∠EAC，即∠BAC=∠EAD，…
  任務：
  （1）托勒密定理的逆命題是

  ；上述證明過程中的“依據1”為

  ；依據2”為

  ；
  （2）請完成后續證明；
  （3）如圖2，以AB為直徑的⊙O中，點C為⊙O上一點，且∠ABC=30°，∠ACB的角平分線交⊙O于點D，連接AD，BD，若AB=4，求CD的長．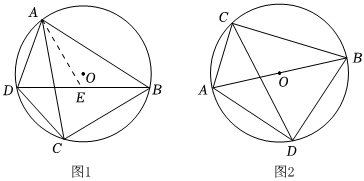
  
  組卷：606引用：2難度：0.4

  解析

• 23．如圖1，矩形ABCD中，AB=4，AD=3，點E為AB的中點，點M為射線DC上一個動點，連接AM，以點E為圓心，以AE的長為半徑作弧，交AM于點N，連接BN，作射線CN交AD于點F．
  （1）判斷：∠ANB的度數為

  °；
  （2）如圖2，當點M為CD的中點時，判斷線段NF與線段AF的數量關系并說明理由；
  （3）如圖3，點G為AD上一點，且DG=1，當∠CNG=90° 時，直接寫出DM的長．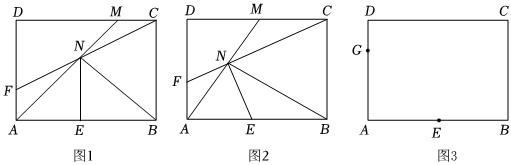
  
  組卷：41引用：1難度：0.2

  解析