閱讀理解：如圖1，在四邊形ABCD中，AB∥DC，點E是BC的中點，若AE是∠BAD的平分線，試判斷AB，AD，DC之間的等量關系．
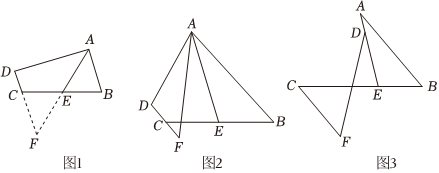
（1）解決此問題可以用如下方法：延長AE交DC的延長線于點F，易證△AEB≌△FEC，得到AB=FC，從而把AB，AD，DC轉化在一個三角形中，即可判斷．AB，AD，DC之間的等量關系為 AD=AB+DCAD=AB+DC；
（2）問題探究：如圖2，在四邊形ABCD中，AB∥DC，AF與DC的延長線交于點F，點E是BC的中點，若AE是∠BAF的平分線，試探究AB，AF，CF之間的等量關系，并證明你的結論；
（3）問題解決：如圖3，AB∥CF，AE與BC交于點E，BE：EC=2：3，點D在線段AE上，且∠EDF=∠BAE，試判斷AB，DF，CF之間的數量關系，直接寫出你的結論．
【考點】四邊形綜合題．
【答案】AD=AB+DC
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/5/7 8:0:9組卷：245引用：2難度：0.1
相似題
-
1．已知在四邊形ABCD中，∠ABC+∠ADC=180°，AB=BC．
（1）如圖1．連接BD，若∠BAD=90°，求證：AD=CD．
（2）如圖2，點P，Q分別在線段AD，DC上，滿足PQ=AP+CQ，求證：∠PBQ=∠ABP+∠QBC；
（3）若點Q在DC的延長線上，點P在DA的延長線上，如圖3所示，仍然滿足PQ=AP+CQ，請寫出∠PBQ與∠ADC的數量關系，并給出證明過程．
發布：2025/6/3 0:0:1組卷：434引用：2難度：0.3 -
2．【教材呈現】如圖是華師版九年級上冊數學教材第77頁的部分內容．
（1）【定理證明】請根據教材內容，結合圖①，寫出證明過程．猜想：如圖，在△ABC中，點D、E分別是AB與AC的中點．
根據畫出的圖形，可以猜想：
DE∥BC，且DE=BC．12
對此，我們可以用演繹推理給出證明．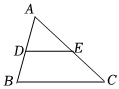
（2）【定理應用】如圖②，已知矩形ABCD中，AD=6，CD=4，點P在BC上從B向C移動，R、E、F分別是DC、AP、RP的中點，則EF=．
（3）【拓展提升】在△ABC中，AB=12，點E是AC的中點，過點A作∠ABC平分線的垂線，垂足為點F，連結EF，若EF=2，則BC=．
發布：2025/6/3 4:30:1組卷：258引用：2難度：0.2 -
3．探究：如圖①，在△ABC中，∠BAC=90°，AB=AC，直線m經過點A，BD⊥m于點D，CE⊥m于點E，求證：△ABD≌△CAE．
應用：如圖②，在△ABC中，AB=AC，D、A、E三點都在直線m上，并且有∠BDA=∠AEC=∠BAC．
求出DE、BD和CE的關系．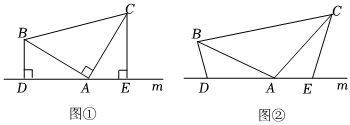
拓展：如圖①中，若DE=10．梯形BCED的面積 ．發布：2025/6/3 1:0:1組卷：94引用：1難度：0.4