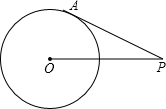
如圖，PA切⊙O于A，⊙O的半徑為3，OP=5，則切線長PA為（ ）
【考點】切線的性質(zhì)；勾股定理．
【答案】C
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2025/6/23 15:0:2組卷：113引用：4難度：0.9
相似題
-
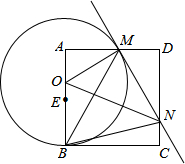1．如圖，已知正方形ABCD，點E是邊AB的中點，點O是線段AE上的一個動點（不與A、E重合），以O(shè)為圓心，OB為半徑的圓與邊AD相交于點M，過點M作⊙O的切線交DC于點N，連接OM、ON、BM、BN．記△MNO、△AOM、△DMN的面積分別為S1、S2、S3，則下列結(jié)論不一定成立的是（ ）發(fā)布：2025/6/23 23:0:10組卷：1674引用：65難度：0.5 -
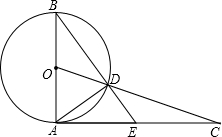2．如圖，AB是⊙O的直徑，過點A作⊙O的切線并在其上取一點C，連接OC交⊙O于點D，BD的延長線交AC于E，連接AD．
（1）求證：△CDE∽△CAD；
（2）若AB=2，AC=2，求AE的長．2發(fā)布：2025/6/23 23:0:10組卷：1653引用：66難度：0.3 -
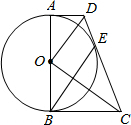3．如圖，在梯形ABCD中，AD∥BC，∠B=90°，以AB為直徑作⊙O，恰與另一腰CD相切于點E，連接OD、OC、BE．
（1）求證：OD∥BE；
（2）若梯形ABCD的面積是48，設(shè)OD=x,OC=y,且x+y=14，求CD的長．發(fā)布：2025/6/23 23:30:1組卷：2062引用：61難度：0.3
相關(guān)試卷