如圖，在正方形ABCD中，點E、F、G分別在AB、BC、CD上，且EF⊥FG于F．
（1）求證：△BEF∽△CFG；
（2）若AB=12，AE=3，CF=4，求CG的長．
【考點】相似三角形的判定與性質；正方形的性質．
【答案】（1）見解析； （2）．
32
9
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/6/15 22:30:1組卷：1335引用：7難度：0.4
相似題
-
1．如圖1，若△ABC內一點P滿足∠PAC=∠PBA=∠PCB，則點P為△ABC的布洛卡點．三角形的布洛卡點是法國數學家和數學教育家克洛爾于1816年首次發現，但他的發現并未被當時的人們所注意，1875年，布洛卡點被一個數學愛好者法國軍官布洛卡重新發現，并用他的名字命名．問題：已知在等腰直角三角形DEF中，如圖2，∠EDF=90°，若點Q為△DEF的布洛卡點，DQ=1，則EQ+FQ=（ ）
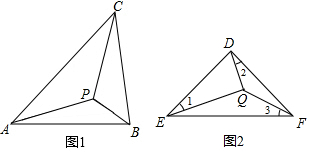
發布：2025/6/16 13:0:5組卷：688引用：3難度：0.6 -
2．矩形ABCD中，長AB與寬BC分別是4cm和3cm,點E在直線AC上，且AE：AC=1：3，直線DE與直線BC相交于點F，則CF的長為 ．
發布：2025/6/16 14:0:1組卷：89引用：1難度：0.3 -
3．定義：如圖①，若點D在△ABC的邊AB上，且滿足∠ACD=∠B，則稱滿足這樣條件的點為△ABC的“理想點”．
（1）如圖①，若點D是△ABC的邊AB的中點，AC=2，AB=4，試判斷點D是不是△ABC的“理想點”，并說明理由；2
（2）如圖②，在Rt△ABC中，∠C=90°，AB=5，AC=4，若點D是△ABC的“理想點”，求CD的長．發布：2025/6/16 14:0:1組卷：372引用：1難度：0.5