 如圖,在?ABCD中,點E、F分別是AD、BC的中點,分別連接BE、DF、BD.
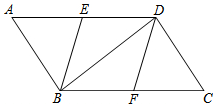
如圖,在?ABCD中,點E、F分別是AD、BC的中點,分別連接BE、DF、BD.
(1)求證:△AEB≌△CFD;
(2)當△ABD滿足什么條件時,四邊形EBFD是菱形,請說明理由.
【答案】(1)證明見解析;
(2)∠ABD=90°,理由見解析.
(2)∠ABD=90°,理由見解析.
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2025/6/7 4:30:1組卷:574引用:4難度:0.5
相似題
-
 1.已知:如圖,在正方形ABCD中,點E、F分別在BC和CD上,AE=AF.
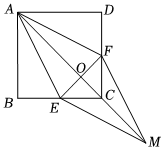
1.已知:如圖,在正方形ABCD中,點E、F分別在BC和CD上,AE=AF.
(1)求證:BE=DF;
(2)連接AC交EF于點O,延長OC至點M,使OM=OA,連接EM,FM,判斷四邊形AEMF是什么特殊四邊形?并證明你的結論.發布:2025/6/7 11:30:1組卷:2744引用:101難度:0.1 -
 2.如圖,在四邊形ABCD中,AD∥BC,AD=CD,E是對角線BD上一點,且EA=EC.求證:四邊形ABCD是菱形.發布:2025/6/7 14:30:1組卷:190引用:3難度:0.5
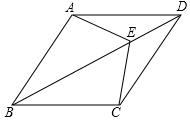
2.如圖,在四邊形ABCD中,AD∥BC,AD=CD,E是對角線BD上一點,且EA=EC.求證:四邊形ABCD是菱形.發布:2025/6/7 14:30:1組卷:190引用:3難度:0.5 -
 3.如圖,在?ABCD中,AC⊥CD.
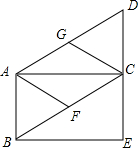
3.如圖,在?ABCD中,AC⊥CD.
(1)延長DC到E,使CE=CD,連接BE,求證:四邊形ABEC是矩形;
(2)若點F,G分別是BC,AD的中點,連接AF,CG,試判斷四邊形AFCG是什么特殊的四邊形?并證明你的結論.發布:2025/6/7 10:0:1組卷:413引用:6難度:0.3


