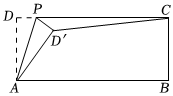
矩形紙片ABCD中，AB=12，AD=5，P為DC上一動點，將△APD沿AP折疊后得到△APD′，連接CD′，則CD′的最小值為 88．
【考點】翻折變換（折疊問題）；矩形的性質．
【答案】8
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/6/4 10:30:2組卷：198引用：2難度：0.7
相似題
-
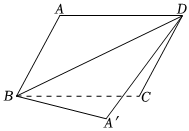1．如圖，將?ABCD沿BD翻折得到△A′BD，若∠ABD=37°，∠CDA′=12°，則∠A′的度數為 ．發布：2025/6/6 7:0:2組卷：128引用：2難度：0.5 -
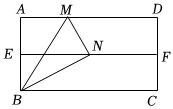2．如圖，對折矩形紙片ABCD，使AD與BC重合，得到折痕EF，把紙片展開．再一次折疊紙片，使點A落在EF上，得到折痕BM，同時，得到線段BN，若AB=，則BM的長為（ ）3發布：2025/6/6 7:0:2組卷：149引用：5難度：0.7 -
3．我們知道平行四邊形那有很多性質，現在如果我們把平行四邊形沿著它的一條對角線翻折，會發現這其中還有更多的結論
【發現與證明】
在?ABCD中，AB≠BC，將△ABC沿AC翻折至△AB′C，連接B′D．
結論1：B′D∥AC；
結論2：△AB′C與?ABCD重疊部分的圖形是等腰三角形．…
請利用圖1證明結論1或結論2．
【應用與探究】
在?ABCD中，∠B=30°，將△ABC沿AC翻折至△AB′C，連接B′D．已知AB=2，當BC的長為 時，△AB′D是直角三角形．3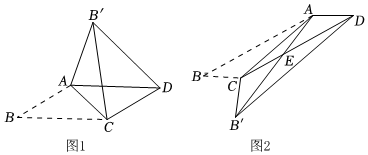
發布：2025/6/6 6:30:1組卷：123引用：1難度：0.4