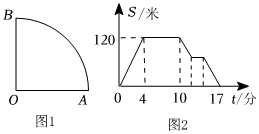
 李大爺在如圖1所示扇形湖畔的棧道上散步,他從圓心O出發(fā),沿O→A→B→O勻速運動,最后回到點O,其中路徑AB是一段長180米的圓弧.李大爺離出發(fā)點O的直線距離S(米)與運動時間t(分)之間的關系如圖2所示.
李大爺在如圖1所示扇形湖畔的棧道上散步,他從圓心O出發(fā),沿O→A→B→O勻速運動,最后回到點O,其中路徑AB是一段長180米的圓弧.李大爺離出發(fā)點O的直線距離S(米)與運動時間t(分)之間的關系如圖2所示.
(1)在 0~4分鐘0~4分鐘時間段內(nèi),李大爺離出發(fā)點O的距離在增大;在4~10分這個時間段內(nèi),李大爺在 ABAB路段上運動(填OA、AB或OB);李大爺從點O出發(fā)到回到點O一共用了 1717分鐘;
(2)扇形線道的半徑是 120120米,李大帶的速度為 3030米/分;
(3)在與出發(fā)點O距離75米處有一個報刊亭,已知李大爺在買報紙前后始終保持運動速度不變,則李大爺是在第 11.511.5分到達報利亭,他在報刊亭停留了 33分鐘.
【考點】圓的綜合題.
【答案】0~4分鐘;AB;17;120;30;11.5;3
【解答】
【點評】
聲明:本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有,未經(jīng)書面同意,不得復制發(fā)布。
發(fā)布:2025/6/4 16:30:1組卷:19引用:1難度:0.3
相似題
-
1.如圖1,以點O為圓心,半徑為4的圓交x軸于A,B兩點,交y軸于C,D兩點,點P為劣弧AC上的一動點,延長CP交x軸于點E;連接PB,交OC于點F.
(1)若點F為OC的中點,求PB的長;
(2)求CP?CE的值;
(3)如圖2,過點O作OH∥AP交PD于點H,當點P在弧AC上運動時,連接AC,PC.試問△APC與△OHD相似嗎?說明理由;的值是否保持不變?若不變,試證明,求出它的值;若發(fā)生變化,請說明理由.APDH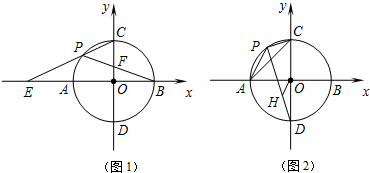 發(fā)布:2025/6/24 18:30:1組卷:272引用:1難度:0.5
發(fā)布:2025/6/24 18:30:1組卷:272引用:1難度:0.5 -
 2.如圖,已知⊙O′與x軸交于A、B兩點,與y軸交于C、D兩點,圓心O′的坐標是(1,-1),半徑為.5
2.如圖,已知⊙O′與x軸交于A、B兩點,與y軸交于C、D兩點,圓心O′的坐標是(1,-1),半徑為.5
(1)比較線段AB與CD的大小;
(2)求A、B、C、D四點的坐標;
(3)過點D作⊙O′的切線,試求這條切線的解析式.發(fā)布:2025/6/24 20:0:2組卷:43引用:1難度:0.5 -
3.下面是“用三角板畫圓的切線”的畫圖過程.
如圖1,已知圓上一點A,畫過A點的圓的切線.畫法:
(1)如圖2,將三角板的直角頂點放在圓上任一點C(與點A不重合)處,使其一直角邊經(jīng)過點A,另一條直角邊與圓交于B點,連接AB;
(2)如圖3,將三角板的直角頂點與點A重合,使一條直角邊經(jīng)過點B,畫出另一條直角邊所在的直線AD.則直線AD就是過點A的圓的切線.
請回答:①這種畫法是否正確 (是或否);
②你判斷的依據(jù)是:.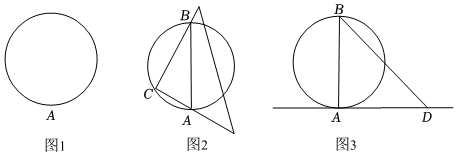 發(fā)布:2025/6/25 8:0:1組卷:19引用:1難度:0.4
發(fā)布:2025/6/25 8:0:1組卷:19引用:1難度:0.4


