已知函數f（x）=e^x-1，g（x）=lnx+1．
（1）判斷函數F（x）=ln[f（x）]+g（x）在其定義域上的單調性（不需要證明）；
（2）對任意的a∈（
1
e
，+∞），都有
f
（
b
）
g
（
a
）
=
a
b
，若存在a的兩個取值a₁，a₂（a₁≠a₂），使得|b-2|=c（c為常數），求a₁?a₂的值．

【答案】（1）F（x）=x+lnx在（0，+∞）上單調遞增；
（2）a₁?a₂=e²．

【解答】

【點評】

聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。

發布：2024/4/20 14:35:0組卷：83引用：3難度：0.3

相似題

1．已知函數f（x）=x³-2kx²+x-3在R上不單調，則k的取值范圍是
；
發布：2024/12/29 13:0:1組卷：237引用：3難度：0.8
解析
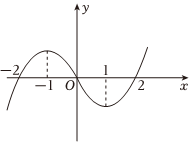2．在R上可導的函數f（x）的圖象如圖示，f′（x）為函數f（x）的導數，則關于x的不等式x?f′（x）＜0的解集為（　　）
A．（-∞，-1）∪（0，1） B．（-2，-1）∪（1，2）
C．（-1，0）∪（1，+∞） D．（-∞，-2）∪（2，+∞）
發布：2024/12/29 13:0:1組卷：265引用：7難度：0.9
解析
3．已知函數f（x）=ax²+x-xlnx（a∈R）
（Ⅰ）若函數f（x）在（0，+∞）上單調遞增，求實數a的取值范圍；
（Ⅱ）若函數f（x）有兩個極值點x₁，x₂（x₁≠x₂），證明：
x
1
?
x
2
＞
e
2
．
發布：2024/12/29 13:30:1組卷：144引用：2難度：0.2
解析

相關試卷

A．（-∞，-1）∪（0，1）	B．（-2，-1）∪（1，2）
C．（-1，0）∪（1，+∞）	D．（-∞，-2）∪（2，+∞）

1．已知函數f（x）=x3-2kx2+x-3在R上不單調，則k的取值范圍是 ；