某商品現(xiàn)在的售價為每件50元，每星期可賣出500件，市場調(diào)查反映：售價每上漲1元，每星期要少賣出10件，已知商品的進價為每件40元，設銷售單價為每件x元（x≥50），每星期的銷售量為y件．
（1）寫出y與x的函數(shù)解析式，并直接寫出x的取值范圍；
（2）商店要使每星期銷售利潤為8000元，銷售價應為每件多少元？
（3）當銷售價定為每件多少元時，每星期獲得利潤最大？最大利潤為多少元？
【考點】二次函數(shù)的應用；一元二次方程的應用．
【答案】（1）y=-10x+1000，50≤x≤100；
（2）銷售價定為每件60元或80元時利潤為8000元；
（3）售價定為70元時，每星期獲得利潤最大，最大利潤為9000元．
（2）銷售價定為每件60元或80元時利潤為8000元；
（3）售價定為70元時，每星期獲得利潤最大，最大利潤為9000元．
【解答】
【點評】
聲明：本試題解析著作權屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：197引用：2難度：0.6
相似題
-
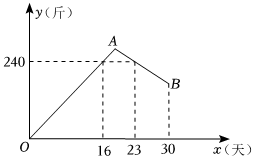1．小明家今年種植的草莓喜獲豐收，該草莓上市的成本價為10元/斤，售價為16元/斤，小明對該草莓一個月（30天）銷售情況進行記錄并繪成如圖所示的圖象．
圖中的折線OAB表示日銷量y（斤）與銷售時間x（天）之間的函數(shù)關系，若線段AB表示的函數(shù)關系中，時間每增加1天，日銷量減少20斤．
（1）第25天的日銷量是 斤，這天銷售利潤是 元；
（2）求y與x之間的函數(shù)關系式，并寫出x的取值范圍；
（3）日銷售利潤不低于1080元的天數(shù)共有多少天？銷售期間日銷售最大利潤是多少元？發(fā)布：2025/5/23 11:0:1組卷：210引用：1難度：0.4 -
2．根據(jù)《平頂山市志》記載，中興路湛河橋是“市區(qū)第一座橫跨湛河的大橋”．已知該橋的橋拱為拋物線形，在正常水位時測得水面AB的寬為50m,最高點C距離水面10m,如圖所示以AB所在的直線為x軸，AB的中點為原點建立平面直角坐標系．
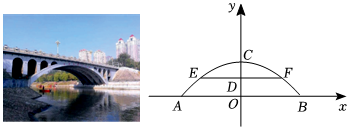
（1）求該拋物線的表達式；
（2）某次大雨后水面上漲至EF，測得最高點C距離EF的高度為3.6m,求橋拱下水面EF的寬度．發(fā)布：2025/5/23 9:30:1組卷：331引用：2難度：0.5 -
3．某超市銷售一種成本為30元/千克的食品，第x天的銷售價格為m元/千克，銷售量為n千克，如表是整理后的部分數(shù)據(jù)．
（1）直接寫出m關于x的函數(shù)解析式和n關于x的函數(shù)解析式 （不要求寫出自變量的取值范圍）．時間x/天 1 5 10 20 … 銷售價格m/（元/千克） 54.5 52.5 50 45 … 銷售量n/千克 66 90 120 180 …
（2）當30≤x≤40時，求第幾天的銷售利潤最大？最大利潤是多少？
（3）如果該超市把銷售價格在當天的基礎上提高a元/千克（原銷售量不變），那么前25天（包含第25天）每天的銷售利潤隨x的增大而增大，請直接寫出a的取值范圍 ．發(fā)布：2025/5/23 9:30:1組卷：376引用：3難度：0.4