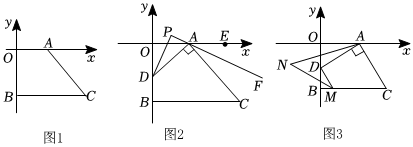
如圖1，在平面直角坐標系中，A（a,0）是x軸正半軸上一點，C是第四象限一點，CB⊥y軸，交y軸負半軸于B（0，b），且（a-3）2+b+4=0，四邊形AOBC的面積是16．
（1）求C點的坐標．
（2）如圖2，設D為線段OB上一動點，當AD⊥AC時，∠ODA的角平分線與∠CAE的角平分線的反向延長線交于點P，求∠APD的度數．
（3）如圖3，當D點在線段OB上運動時，作DM⊥AD交BC于M點，∠BMD、∠DAO的平分線交于N點，則D在運動過程中，∠N的大小是否變化？若不變，求出其值，若變化，請說明理由．
???
（
a
-
3
）
2
+
b
+
4
=
0
【考點】四邊形綜合題．
【答案】（1）C（5，-4）；
（2）90°；
（3）45°．
（2）90°；
（3）45°．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/6/6 9:30:1組卷：135引用：1難度：0.1
相似題
-
1．在線上教學中，教師和學生都學習到了新知識，掌握了許多新技能．例如教材八年級下冊的數學活動一折紙，就引起了許多同學的興趣．在經歷圖形變換的過程中，進一步發展了同學們的空間觀念，積累了數學活動經驗．
實踐發現：
對折矩形紙片ABCD，使AD與BC重合，得到折痕EF，把紙片展平；再一次折疊紙片，使點A落在EF上的點N處，并使折痕經過點B，得到折痕BM，把紙片展平，連接AN，如圖①．
（1）①計算出∠MNE=°；
②繼續折疊紙片，使點A落在BC邊上的點H處，并使折痕經過點B，得到折痕BG，把紙片展平，如圖②，則∠GBN=°；
拓展延伸：
（2）如圖③，折疊矩形紙片ABCD，使點A落在BC邊上的點A'處，并且折痕交BC邊于點T，交AD邊于點S，把紙片展平，連接AA'交ST于點O，連接AT．求證：四邊形SATA'是菱形；
解決問題：
（3）如圖④，矩形紙片ABCD中，AB=10，AD=26，折疊紙片，使點A落在BC邊上的點A'處，并且折痕交AB邊于點T，交AD邊于點S，把紙片展平．同學們小組討論后，得出線段AT的長度有4，5，7，9．
請寫出以上4個數值中你認為正確的數值 ．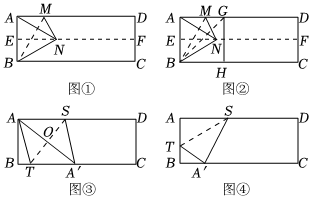
發布：2025/6/7 2:30:1組卷：127引用：1難度：0.3 -
2．已知正方形ABCD的邊長為4，△BEF為等邊三角形，點E在AB邊上，點F在AB邊的左側．
（1）如圖1，若D，E，F在同一直線上，求BF的長；
（2）如圖2，連接AF，CE，BD，并延長CE交AF于點H，若CH⊥AF，求證：AE+2FH=BD；2
（3）如圖3，將△ABF沿AB翻折得到△ABP，點Q為AP的中點，連接CQ，若點E在射線BA上運動時，請直接寫出線段CQ的最小值．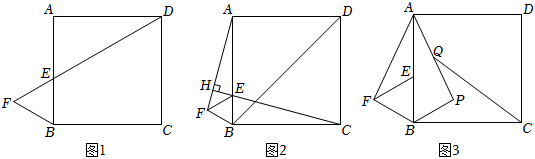
發布：2025/6/7 2:0:5組卷：1043引用：10難度：0.2 -
3．探究問題．
（1）方法感悟：
如圖①，在正方形ABCD中，點E，F分別為DC，BC邊上的點，且滿足∠EAF=45°，連接EF，求證：DE+BF=EF．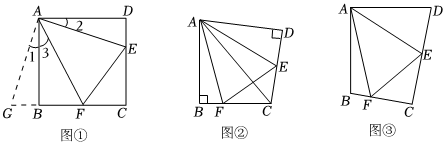
感悟解題方法，并完成下列填空：
將△ADE繞點A順時針旋轉90°得到△ABG，此時AB與AD重合，由旋轉可得：AB=AD，BG=DE，∠1=∠2，∠ABG=∠D=90°，
∴∠ABG+∠ABF=90°+90°=180°，
因此，點G，B，F在同一條直線上．
∵∠EAF=45°，
∴∠2+∠3=．
∵∠1=∠2，
∴∠1+∠3=45°，即∠GAF=∠EAF．
又AG=AE，AF=AF，
△GAE≌．
∴GF=EF，故DE+BF=EF．
（2）方法遷移：
如圖②，將Rt△ABC沿斜邊翻折得到△ADC，點E，F分別為DC，BC邊上的點，且∠EAF=∠DAB．試猜想DE，BF，EF之間有何數量關系，并證明你的猜想．12
（3）問題拓展：
如圖③，在四邊形ABCD中，AB=AD，E，F分別為DC，BC上的點，滿足∠EAF=∠DAB，試猜想當∠B與∠D滿足什么關系時，可使得DE+BF=EF．請直接寫出你的猜想（不必說明理由）．12發布：2025/6/7 1:0:2組卷：119引用：1難度：0.1