【問題提出】用n根相同的木棒搭一個三角形(木棒無剩余),能搭成多少種不同的等腰三角形?
【問題探究】不妨假設能搭成m種不同的等腰三角形,為探究m與n之間的關系,我們可以先從特殊入手,通過試驗、觀察、類比、最后歸納、猜測得出結論.
【探究一】
(1)用3根相同的木棒搭一個三角形,能搭成多少種不同的等腰三角形?
此時,顯然能搭成一種等腰三角形.
所以,當n=3時,m=1.
(2)用4根相同的木棒搭一個三角形,能搭成多少種不同的等腰三角形?
只可分成1根木棒、1根木棒和2根木棒這一種情況,不能搭成三角形.
所以,當n=4時,m=0.
(3)用5根相同的木棒搭一個三角形,能搭成多少種不同的等腰三角形?
若分成1根木棒、1根木棒和3根木棒,則不能搭成三角形.
若分成2根木棒、2根木棒和1根木棒,則能搭成一種等腰三角形.
所以,當n=5時,m=1.
(4)用6根相同的木棒搭一個三角形,能搭成多少種不同的等腰三角形?
若分成1根木棒、1根木棒和4根木棒,則不能搭成三角形.
若分成2根木棒、2根木棒和2根木棒,則能搭成一種等腰三角形.
所以,當n=6時,m=1.
綜上所述,可得:表①
| n | 3 | 4 | 5 | 6 |
| m | 1 | 0 | 1 | 1 |
(1)用7根相同的木棒搭一個三角形,能搭成多少種不同的三角形?
(仿照上述探究方法,寫出解答過程,并將結果填在表②中)
(2)用8根、9根、10根相同的木棒搭一個三角形,能搭成多少種不同的等腰三角形?
(只需把結果填在表②中)
表②
| n | 7 | 8 | 9 | 10 |
| m | 2 2 | 1 1 | 2 2 | 2 2 |
【問題解決】:用n根相同的木棒搭一個三角形(木棒無剩余),能搭成多少種不同的等腰三角形?(設n分別等于4k-1,4k,4k+1,4k+2,其中k是正整數,把結果填在表③中)
表③
| n | 4k-1 | 4k | 4k+1 | 4k+2 |
| m | k k | k-1 k-1 | k k | k k |
672
672
根木棒.(只填結果)【答案】2;1;2;2;k;k-1;k;k;672
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/4/20 14:35:0組卷:779引用:28難度:0.3
相似題
-
1.如圖,△ABC是正方形網格圖中的格點三角形(頂點在格點上),請按要求作圖:
(1)在圖1中,過點C作與AB平行的格點線段CE.
(2)在圖2中,以AB為邊作Rt△ABE,使它的一個銳角等于∠B,且與△ABC不全等.
(3)在圖3中,在AB,BC邊上取點G,H,將△ABC折疊,使點B與點A重合,畫出線段AH.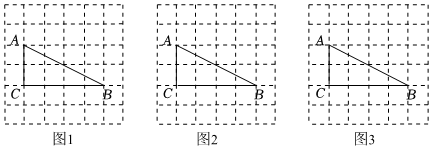 發布:2025/5/25 18:30:1組卷:56引用:1難度:0.5
發布:2025/5/25 18:30:1組卷:56引用:1難度:0.5 -
 2.如圖,方格紙中每個小正方形的邊長均為1,線段AB和線段CD的端點均在小正方形的頂點上.
2.如圖,方格紙中每個小正方形的邊長均為1,線段AB和線段CD的端點均在小正方形的頂點上.
(1)在圖中畫出以AB為邊的正方形ABEF,點E和點F均在小正方形的頂點上;
(2)在圖中畫出以CD為邊的等腰三角形CDG,點G在小正方形的頂點上,且△CDG的周長為10+.連接EG,請直接寫出線段EG的長.10發布:2025/5/25 19:0:2組卷:356引用:13難度:0.5 -
3.圖①、圖②、圖③均是5×5的正方形網格,每個小正方形的邊長均為1,每個小正方形的頂點稱為格點,點A、B均在格點上.在圖①、圖②、圖③中,只用無刻度的直尺,在給定的網格中按要求作圖,所畫圖形的頂點均在格點上.
(1)在圖①中,畫等腰三角形ABC,使其面積為3.
(2)在圖②中,畫等腰直角三角形ABD,使其面積為5.
(3)在圖③中,畫平行四邊形ABEF,使其面積為9.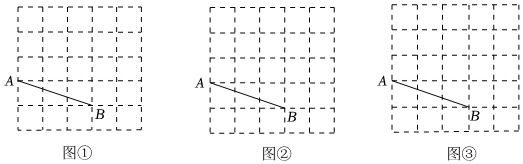 發布:2025/5/25 18:0:1組卷:253引用:3難度:0.5
發布:2025/5/25 18:0:1組卷:253引用:3難度:0.5


