2020-2021學年浙江省杭州市蕭山實驗中學八年級（上）月考數學試卷（10月份）

一、選擇題（共十題：共30分）

• 1．下列語句是命題的是（　　）

  A．作直線AB的垂線	B．同旁內角互補
  C．在線段AB上取點C	D．垂線段最短嗎？
  組卷：308引用：46難度：0.9

  解析

• 2．如果等腰三角形一個底角是30°，那么頂角是（　　）

  A．60°

  B．150°

  C．120°

  D．75°
  組卷：28引用：4難度：0.9

  解析

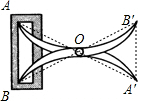• 3．如圖，將兩根鋼條AA'、BB'的中點O連在一起，使AA'、BB'可以繞著點O自由旋轉，就做成了一個測量工件，則A'B'的長等于內槽寬AB，那么判定△OAB≌△OA'B'的理由是（　　）

  A．SSS

  B．SAS

  C．AAS

  D．ASA
  組卷：1259引用：24難度：0.5

  解析

• 4．下列四個關于軸對稱的判斷①對稱軸可以是直線、線段或射線；②軸對稱圖形的對稱軸至少有一條；③成軸對稱的兩個圖形全等，全等的兩個圖形成軸對稱；④線段是軸對稱圖形中，正確的是（　　）

  A．①②

  B．②③

  C．①③

  D．②④
  組卷：11引用：1難度：0.8

  解析

• 5．已知△A₁B₁C₁，△A₂B₂C₂的周長相等，現有兩個判斷：①若A₁B₁=A₂B₂，A₁C₁=A₂C₂，則△A₁B₁C₁≌△A₂B₂C₂；②若A₁B₁=A₂B₂，∠A₁=∠A₂，則△A₁B₁C₁≌△A₂B₂C₂，對于上述的兩個判斷，下列說法正確的是（　　）

  A．①正確，②錯誤	B．①錯誤，②正確
  C．①②都錯誤	D．①②都正確
  組卷：27引用：1難度：0.5

  解析

• 6．一個等腰三角形的底邊長為5，一腰上中線把其周長分成的兩部分的差為3，則這個等腰三角形的腰長為（　　）

  A．2

  B．8

  C．2或8

  D．10
  組卷：190引用：5難度：0.9

  解析

• 7．在等腰三角形中，AB的長是BC的2倍，周長為40，則AB的長為（　　）

  A．16

  B．20

  C．16或20

  D．以上都不對
  組卷：429引用：6難度：0.9

  解析

三、解答題（共七題：共66分）

• 22．已知等腰△ABC中，∠A=80°．
  （1）求∠B的度數．
  （2）在解答完（1）后，小敏發現，∠A的度數不同，得到∠B的度數的個數也可能不同，如果在等腰△ABC中，設∠A=x°，當∠B有三個不同的度數時，請你探索x的取值范圍．
  組卷：9引用：1難度：0.5

  解析

• 23．【問題提出】用n根相同的木棒搭一個三角形（木棒無剩余），能搭成多少種不同的等腰三角形？
  【問題探究】不妨假設能搭成m種不同的等腰三角形，為探究m與n之間的關系，我們可以先從特殊入手，通過試驗、觀察、類比、最后歸納、猜測得出結論．
  【探究一】
  （1）用3根相同的木棒搭一個三角形，能搭成多少種不同的等腰三角形？
  此時，顯然能搭成一種等腰三角形．
  所以，當n=3時，m=1．
  （2）用4根相同的木棒搭一個三角形，能搭成多少種不同的等腰三角形？
  只可分成1根木棒、1根木棒和2根木棒這一種情況，不能搭成三角形．
  所以，當n=4時，m=0．
  （3）用5根相同的木棒搭一個三角形，能搭成多少種不同的等腰三角形？
  若分成1根木棒、1根木棒和3根木棒，則不能搭成三角形．
  若分成2根木棒、2根木棒和1根木棒，則能搭成一種等腰三角形．
  所以，當n=5時，m=1．
  （4）用6根相同的木棒搭一個三角形，能搭成多少種不同的等腰三角形？
  若分成1根木棒、1根木棒和4根木棒，則不能搭成三角形．
  若分成2根木棒、2根木棒和2根木棒，則能搭成一種等腰三角形．
  所以，當n=6時，m=1．
  綜上所述，可得：表①
  

  n	3	4	5	6
  m	1	0	1	1

  【探究二】
  （1）用7根相同的木棒搭一個三角形，能搭成多少種不同的三角形？
  （仿照上述探究方法，寫出解答過程，并將結果填在表②中）
  （2）用8根、9根、10根相同的木棒搭一個三角形，能搭成多少種不同的等腰三角形？
  （只需把結果填在表②中）
  表②
  

  n	7	8	9	10
  m

  你不妨分別用11根、12根、13根、14根相同的木棒繼續進行探究，…
  【問題解決】：用n根相同的木棒搭一個三角形（木棒無剩余），能搭成多少種不同的等腰三角形？（設n分別等于4k-1，4k,4k+1，4k+2，其中k是正整數，把結果填在表③中）
  表③
  

  n	4k-1	4k	4k+1	4k+2
  m

  【問題應用】：用2016根相同的木棒搭一個三角形（木棒無剩余），能搭成多少種不同的等腰三角形？（寫出解答過程），其中面積最大的等腰三角形每腰用了

   

  根木棒．（只填結果）
  組卷：779引用：28難度：0.3

  解析