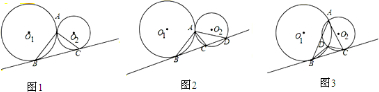
已知⊙O1和⊙O2外切于A（如圖1），BC是它們的一條外公切線，B、C分別為切點，連接AB、AC，
（1）求證：AB⊥AC；
（2）將兩圓外公切線BC變為⊙O1的切線，且為⊙O2的割線BCD（如圖2），其它條件不變，猜想∠BAC+∠BAD的大小，并加以證明；
（3）將兩圓外切變為兩圓相交于A、D（如圖3），其它條件不變，猜想：∠BAC+∠BDC的大小？并加以證明．
【答案】見試題解答內容
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/5/29 6:30:1組卷：107引用：1難度：0.3
相似題
-
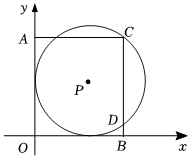1．如圖，在平面直角坐標系中，點P在第一象限，⊙P與x軸、y軸都相切，且經過矩形AOBC的頂點C，與BC相交于點D，若⊙P的半徑為5，點A的坐標是（0，9），則點D的坐標是 ．發布：2025/5/30 12:0:2組卷：549引用：3難度：0.5 -
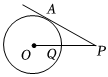2．如圖，PA與⊙O相切于點A，連接OP，交⊙O于點Q，若AP=12，PQ=8，則⊙O的半徑為 ．發布：2025/5/30 13:0:1組卷：42引用：1難度：0.7 -
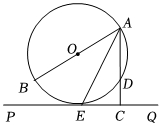3．如圖，AB為⊙O的直徑，PQ切⊙O于E，AC⊥PQ于C，交⊙O于D．
（1）求證：AE平分∠BAC；
（2）若，∠BAC=60°，求⊙O的半徑．EC=3發布：2025/5/30 13:0:1組卷：514引用：5難度：0.6