在整式乘法的學(xué)習(xí)中，我們采用了構(gòu)造幾何圖形的方法研究代數(shù)式的變形問題．現(xiàn)有邊長(zhǎng)分別為a,b的正方形Ⅰ號(hào)和Ⅱ號(hào)卡片，以及長(zhǎng)為a,寬為b的長(zhǎng)方形Ⅲ號(hào)卡片，這些卡片足夠多，我們可以選取適量的卡片拼接成幾何圖形（卡片間不重疊、無縫隙）．根據(jù)已有的學(xué)習(xí)經(jīng)驗(yàn)，解決下列問題：
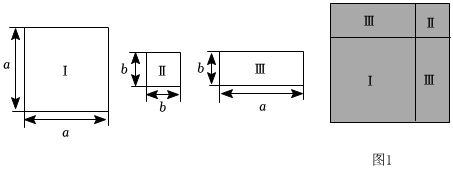
（1）圖1是由1張Ⅰ號(hào)卡片、1張Ⅱ號(hào)卡片、2張Ⅲ號(hào)卡片拼接成的大正方形，用兩種不同的方法表示圖1中陰影部分面積，可以得到一個(gè)等式，請(qǐng)寫出這個(gè)等式 （a+b）2=a2+2ab+b2（a+b）2=a2+2ab+b2．
（2）若要拼出一個(gè)長(zhǎng)方形，使它可以驗(yàn)證等式：（a+2b）（a+b）=a2+3ab+2b2，請(qǐng)畫出這個(gè)圖形．
（3）根據(jù)（1）中的等量關(guān)系，解決如下問題：
①已知：a+b=7，a2+b2=25，求ab的值；
②已知（2022-x）2+（x-2020）2=3，求（2022-x）（x-2020）的值．
【答案】（a+b）2=a2+2ab+b2
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：117引用：1難度：0.4
相似題
-
1．將兩數(shù)和（差）的平方公式：（a±b）2=a2±2ab+b2，通過適當(dāng)?shù)淖冃危梢越鉀Q很多數(shù)學(xué)問題．
例如：若a-b=3，ab=1，求a2+b2的值．
解：∵a-b=3，ab=1，
∴a2+b2=（a-b）2+2ab=32+2×1=11．
請(qǐng)根據(jù)上面的解題思路和方法，解決下列問題：
（1）若x+y=10，x2+y2=56，求xy的值；
（2）將邊長(zhǎng)為x的正方形ABCD和邊長(zhǎng)為y的正方形CEFG按如圖所示放置，其中點(diǎn)D在邊CE上，連接AG，EG，若x+y=8，xy=14，求陰影部分的面積．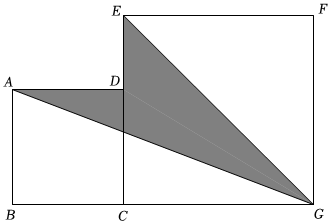
發(fā)布：2025/5/31 9:30:2組卷：1941引用：4難度：0.5 -
2．完全平方公式：（a±b）2=a2±2ab+b2經(jīng)過適當(dāng)?shù)淖冃危梢越鉀Q很多數(shù)學(xué)問題，例如：若a+b=3，ab=1，求a2+b2的值．
解：∵a+b=3，ab=1，∴（a+b）2=9，2ab=2，
∴a2+b2+2ab=9，∴a2+b2=7．
根據(jù)上面的解題思路與方法，解決下列問題：
（1）①若x+y=6，x2+y2=28，則xy=；
②若2a+b=6，ab=4，則（2a-b）2=；
③若（6-x）x=4，則（6-x）2+x2=；
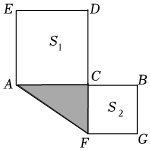
（2）如圖，C是線段AB上的一點(diǎn)，以AC，BC為邊向兩邊作正方形，設(shè)AB=8，兩正方形的面積和S1+S2=44，求△AFC的面積．發(fā)布：2025/5/30 19:30:1組卷：1286引用：10難度：0.6 -
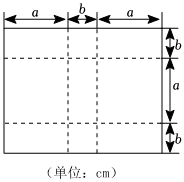3．如圖，將一張長(zhǎng)方形大鐵皮切割成九塊（切痕為虛線），其中有兩塊是邊長(zhǎng)都為a cm的大正方形，兩塊是邊長(zhǎng)都為b cm的小正方形，五塊是長(zhǎng)為a cm、寬為b cm的小長(zhǎng)方形．
（1）這張長(zhǎng)方形大鐵皮的長(zhǎng)為 cm,寬為 cm.（用含a、b的代數(shù)式表示）
（2）求這張長(zhǎng)方形大鐵皮的面積S．（用含a、b的代數(shù)式表示）
（3）若一個(gè)小長(zhǎng)方形的周長(zhǎng)為22cm,一個(gè)大正方形與一個(gè)小正方形的面積之差為33cm2，求a、b的值，并求這張長(zhǎng)方形大鐵皮的面積S．發(fā)布：2025/5/30 15:0:2組卷：344引用：5難度：0.7