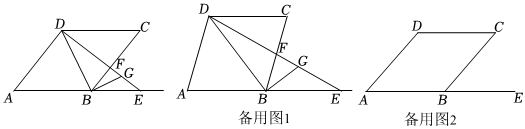
如圖，在菱形ABCD中，AB=5，BD為對角線．點(diǎn)E是邊AB延長線上的任意一點(diǎn)，連結(jié)DE交BC于點(diǎn)F，BG平分∠CBE交DE于點(diǎn)G．
（1）求證：∠DBG=90°．
（2）若BD=6，DG=2GE．
①求菱形ABCD的面積．
②求tan∠BDE的值．
（3）若BE=AB，當(dāng)∠DAB的大小發(fā)生變化時(shí)（0°＜∠DAB＜180°），在AE上找一點(diǎn)T，使GT為定值，說明理由并求出ET的值．
【考點(diǎn)】四邊形綜合題．
【答案】（1）證明過程見解答；
（2）①S菱形ABCD=24；
②tan∠BDE=；
（3）作GT∥BC交AE于點(diǎn)T，點(diǎn)T就是所求的點(diǎn)，理由見解答，ET=．
（2）①S菱形ABCD=24；
②tan∠BDE=
4
9
（3）作GT∥BC交AE于點(diǎn)T，點(diǎn)T就是所求的點(diǎn)，理由見解答，ET=
10
3
【解答】
【點(diǎn)評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：2781引用：5難度：0.3
相似題
-
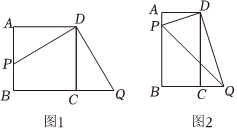1．（1）如圖1，將直角三角板的直角頂點(diǎn)放在正方形ABCD上，使直角頂點(diǎn)與D重合，三角板的一邊交AB于點(diǎn)P，另一邊交BC的延長線于點(diǎn)Q．求證：DP=DQ；
（2）如圖2，將（1）中“正方形ABCD”改成“矩形ABCD”，且DC=2DA，其他條件不變，試猜想DQ與DP的數(shù)量關(guān)系，并說明理由；
（3）在（2）的條件下，若PQ=10，DA=4，則AP的長度為 ．（直接寫出答案）發(fā)布：2025/5/21 17:0:2組卷：60引用：2難度：0.5 -
2．【基礎(chǔ)問題】
如圖①，矩形ABCD中，點(diǎn)E為AB邊上一點(diǎn)，連接DE，作EF⊥DE交BC于點(diǎn)F，且DE=FE，求證：△AED≌△BFE．
【拓展延伸】
（1）如圖②，點(diǎn)E為平行四邊形ABCD內(nèi)部一點(diǎn)，EA=EB，DA⊥AE，作DF⊥BA交BA延長線于點(diǎn)F，若DA=2EA，AB=5，則平行四邊形ABCD的面積為 ；
（2）如圖③，在正方形ABCD中，AD=6，在CD邊上取一點(diǎn)E，使EC=2DE，將△AED沿AE翻折到△AED′位置，作D′F⊥AB于點(diǎn)F，在D′F右側(cè)作∠FGD'=90°，則△FGD'面積的最大值為 ．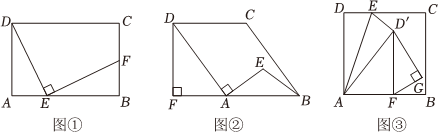
發(fā)布：2025/5/21 17:0:2組卷：160引用：1難度：0.3 -
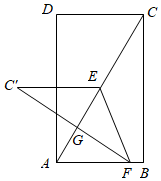3．如圖，矩形ABCD中，AB=2，BC=4，連結(jié)對角線AC，E為AC的中點(diǎn)，F(xiàn)為AB邊上的動(dòng)點(diǎn)，連結(jié)EF，作點(diǎn)C關(guān)于EF的對稱點(diǎn)C′，連結(jié)C′E，C′F，若△EFC′與△ACF的重疊部分（△EFG）面積等于△ACF的3，則BF=．14發(fā)布：2025/5/21 18:0:1組卷：1667引用：8難度：0.1